Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T16:37:50.426Z Has data issue: false hasContentIssue false
  • English
  • Français

CHAIN CONDITIONS ON ÉTALE GROUPOID ALGEBRAS WITH APPLICATIONS TO LEAVITT PATH ALGEBRAS AND INVERSE SEMIGROUP ALGEBRAS

Part of: Semigroups Chain conditions, growth conditions, and other forms of finiteness Topological and differentiable algebraic systems

Published online by Cambridge University Press:  28 March 2018

BENJAMIN STEINBERG
BENJAMIN STEINBERG*
Affiliation:
Department of Mathematics, City College of New York, Convent Avenue at 138th Street, New York, NY 10031, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

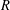The author has previously associated to each commutative ring with unit $R$ and étale groupoid 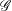$\mathscr{G}$ with locally compact, Hausdorff and totally disconnected unit space an 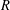$R$-algebra 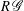$R\,\mathscr{G}$. In this paper we characterize when 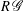$R\,\mathscr{G}$ is Noetherian and when it is Artinian. As corollaries, we extend the characterization of Abrams, Aranda Pino and Siles Molina of finite-dimensional and of Noetherian Leavitt path algebras over a field to arbitrary commutative coefficient rings and we recover the characterization of Okniński of Noetherian inverse semigroup algebras and of Zelmanov of Artinian inverse semigroup algebras.

Keywords

étale groupoidsgroupoid algebraschain conditionsLeavitt path algebrasinverse semigroup algebras

MSC classification

Primary: 16P20: Artinian rings and modules
Secondary: 16P40: Noetherian rings and modules 22A22: Topological groupoids (including differentiable and Lie groupoids) 20M25: Semigroup rings, multiplicative semigroups of rings
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 104 , Issue 3 , June 2018 , pp. 403 - 411
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Abrams, G., ‘Leavitt path algebras: the first decade’, Bull. Math. Sci. 5(1) (2015), 59–120.Google Scholar
Abrams, G., Ara, P. and Siles Molina, M., Leavitt Path Algebras, Lecture Notes in Mathematics, 2191 (Springer, London, 2017).Google Scholar
Abrams, G. and Aranda Pino, G., ‘The Leavitt path algebra of a graph’, J. Algebra 293(2) (2005), 319–334.Google Scholar
Abrams, G., Aranda Pino, G. and Siles Molina, M., ‘Finite-dimensional Leavitt path algebras’, J. Pure Appl. Algebra 209(3) (2007), 753–762.Google Scholar
Abrams, G., Aranda Pino, G. and Siles Molina, M., ‘Locally finite Leavitt path algebras’, Israel J. Math. 165 (2008), 329–348.Google Scholar
Ara, P., Bosa, J., Hazrat, R. and Sims, A., ‘Reconstruction of graded groupoids from graded Steinberg algebras’, Forum Math. 29(5) (2017), 1023–1037.Google Scholar
Ara, P., Hazrat, R., Li, H. and Sims, A., ‘Graded Steinberg algebras and their representations’, Preprint, 2017, arXiv e-prints.Google Scholar
Ara, P., Moreno, M. A. and Pardo, E., ‘Nonstable K-theory for graph algebras’, Algebr. Represent. Theory 10(2) (2007), 157–178.Google Scholar
Beuter, V. and Gonçalves, D., ‘The interplay between Steinberg algebras and partial skew rings’, J. Algebra 497 (2018), 337–362.CrossRefGoogle Scholar
Beuter, V., Gonçalves, D., Öinert, J. and Royer, D., ‘Simplicity of skew inverse semigroup rings with an application to Steinberg algebras’, Preprint, 2017, arXiv e-prints.Google Scholar
Brown, J., Clark, L. O., Farthing, C. and Sims, A., ‘Simplicity of algebras associated to étale groupoids’, Semigroup Forum 88(2) (2014), 433–452.Google Scholar
Brown, J. H., Clark, L. O. and an Huef, A., ‘Purely infinite simple Steinberg algebras have purely infinite simple $C^{\ast }$ -algebras’, Preprint, 2017, arXiv e-prints.Google Scholar
Brown, J. H. and an Huef, A., ‘The socle and semisimplicity of a Kumjian–Pask algebra’, Comm. Algebra 43(7) (2015), 2703–2723.Google Scholar
Carlsen, T. M. and Rout, J., ‘Diagonal-preserving graded isomorphisms of Steinberg algebras’, Commun. Contemp. Math., to appear.Google Scholar
Carlsen, T. M., Ruiz, E. and Sims, A., ‘Equivalence and stable isomorphism of groupoids, and diagonal-preserving stable isomorphisms of graph C ∗ -algebras and Leavitt path algebras’, Proc. Amer. Math. Soc. 145(4) (2017), 1581–1592.Google Scholar
Clark, L. O., Barquero, D. M., González, C. M. and Siles Molina, M., ‘Using the Steinberg algebra model to determine the center of any Leavitt path algebra’, Preprint, 2016, arXiv e-prints.Google Scholar
Clark, L. O., Barquero, D. M., Gonzalez, C. M. and Siles Molina, M., ‘Using Steinberg algebras to study decomposability of Leavitt path algebras’, Forum Math. 29(6) (2017), 1311–1324.Google Scholar
Clark, L. O. and Edie-Michell, C., ‘Uniqueness theorems for Steinberg algebras’, Algebr. Represent. Theory 18(4) (2015), 907–916.Google Scholar
Clark, L. O., Edie-Michell, C., an Huef, A. and Sims, A., ‘Ideals of Steinberg algebras of strongly effective groupoids, with applications to Leavitt path algebras’, Preprint, 2016, arXiv e-prints.Google Scholar
Clark, L. O., Exel, R. and Pardo, E., ‘A generalised uniqueness theorem and the graded ideal structure of Steinberg algebras’, Preprint, 2016, arXiv e-prints.Google Scholar
Clark, L. O., Farthing, C., Sims, A. and Tomforde, M., ‘A groupoid generalisation of Leavitt path algebras’, Semigroup Forum 89(3) (2014), 501–517.Google Scholar
Clark, L. O. and Sims, A., ‘Equivalent groupoids have Morita equivalent Steinberg algebras’, J. Pure Appl. Algebra 219(6) (2015), 2062–2075.CrossRefGoogle Scholar
Connell, I. G., ‘On the group ring’, Canad. J. Math. 15 (1963), 650–685.Google Scholar
Exel, R., ‘Inverse semigroups and combinatorial C ∗ -algebras’, Bull. Braz. Math. Soc. (N.S.) 39(2) (2008), 191–313.Google Scholar
Hazrat, R. and Li, H., ‘Graded Steinberg algebras and partial actions’, Preprint, 2017, arXiv e-prints.Google Scholar
Lawson, M. V., Inverse Semigroups: The Theory of Partial Symmetries (World Scientific, River Edge, NJ, 1998).CrossRefGoogle Scholar
Mitchell, B., ‘Rings with several objects’, Adv. Math. 8 (1972), 1–161.CrossRefGoogle Scholar
Nystedt, P., Öinert, J. and Pinedo, H., ‘Artinian and noetherian partial skew groupoid rings’, Preprint, 2016, arXiv e-prints.Google Scholar
Okniński, J., ‘Noetherian property for semigroup rings’, in: Ring Theory (Granada, 1986), Lecture Notes in Mathematics, 1328 (Springer, Berlin, 1988), 209–218.Google Scholar
Okniński, J., Semigroup Algebras, Monographs and Textbooks in Pure and Applied Mathematics, 138 (Marcel Dekker, New York, 1991).Google Scholar
Paterson, A. L. T., Groupoids, Inverse Semigroups, and Their Operator Algebras, Progress in Mathematics, 170 (Birkhäuser, Boston, MA, 1999).CrossRefGoogle Scholar
Renault, J., A Groupoid Approach to C ∗ -Algebras, Lecture Notes in Mathematics, 793 (Springer, Berlin, 1980).CrossRefGoogle Scholar
Resende, P., ‘Étale groupoids and their quantales’, Adv. Math. 208(1) (2007), 147–209.Google Scholar
Steinberg, B., ‘Möbius functions and semigroup representation theory. II. Character formulas and multiplicities’, Adv. Math. 217(4) (2008), 1521–1557.Google Scholar
Steinberg, B., ‘A groupoid approach to discrete inverse semigroup algebras’, Preprint, 2009, arXiv:0903.3456.Google Scholar
Steinberg, B., ‘A groupoid approach to discrete inverse semigroup algebras’, Adv. Math. 223(2) (2010), 689–727.Google Scholar
Steinberg, B., ‘Modules over étale groupoid algebras as sheaves’, J. Aust. Math. Soc. 97(3) (2014), 418–429.CrossRefGoogle Scholar
Steinberg, B., Representation Theory of Finite Monoids, Universitext (Springer, Cham, 2016).Google Scholar
Steinberg, B., ‘Simplicity, primitivity and semiprimitivity of étale groupoid algebras with applications to inverse semigroup algebras’, J. Pure Appl. Algebra 220(3) (2016), 1035–1054.Google Scholar
Steinberg, B., ‘Diagonal-preserving isomorphisms of étale groupoid algebras’, Preprint, 2017, arXiv e-prints.Google Scholar
Webb, P., ‘An introduction to the representations and cohomology of categories’, in: Group Representation Theory (EPFL Press, Lausanne, 2007), 149–173.Google Scholar
Zelmanov, E. I., ‘Semigroup algebras with identities’, Sibirsk. Mat. Zh. 18(4) (1977), 787–798, 956.Google Scholar