Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-05T15:35:21.473Z Has data issue: false hasContentIssue false
  • English
  • Français

CHAIN COMPONENTS WITH THE STABLE SHADOWING PROPERTY FOR C1 VECTOR FIELDS

Part of: Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  01 February 2021

MANSEOB LEE Open the ORCID record for MANSEOB LEE [Opens in a new window]  and
LE HUY TIEN Open the ORCID record for LE HUY TIEN [Opens in a new window]
MANSEOB LEE
Affiliation:
Department of Mathematics, Mokwon University, Daejeon, 302-729Korea e-mail: [email protected]
LE HUY TIEN
Affiliation:
Department of Mathematics, VNU Hanoi University of Science, 334 Nguyen Trai, Hanoi, Vietnam e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let M be a closed n-dimensional smooth Riemannian manifold, and let X be a 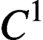$C^1$-vector field of 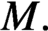$M.$ Let 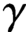$\gamma $ be a hyperbolic closed orbit of 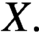$X.$ In this paper, we show that X has the 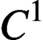$C^1$-stably shadowing property on the chain component 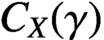$C_X(\gamma )$ if and only if 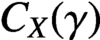$C_X(\gamma )$ is the hyperbolic homoclinic class.

Keywords

shadowingchain componenthomoclinic classstar conditionhyperbolic

MSC classification

Primary: 37D05: Hyperbolic orbits and sets
Secondary: 37D30: Partially hyperbolic systems and dominated splittings 37D50: Hyperbolic systems with singularities (billiards, etc.)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 110 , Issue 2 , April 2021 , pp. 243 - 259
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work is supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT & Future Planning (No. 2017R1A2B4001892). The second author is supported by the VNU Project of Vietnam National University (No. QG.15.01).

References

Abdenur, F. and Díaz, L. J., ‘Pesudo orbit shadowing in the ${C}^1$ topology’, Discrete Contin. Dyn. Syst. 17 (2007), 223–245.CrossRefGoogle Scholar
Ahn, J., Lee, K. and Lee, M., ‘Homoclinic classes with shadowing’, J. Inequal. Appl. 97 (2012), 1–6.Google Scholar
Aoki, N., ‘The set of Axiom A diffeomorphisms with no-cycles’, Bol. Soc. Bras. Mat. 23 (1992), 21–65.CrossRefGoogle Scholar
Arbieto, A., Senos, L. and Sodero, T., ‘The specification property for flows from the robust and generic viewpoint’, J. Differential Equations 253 (2012), 1893–1909.CrossRefGoogle Scholar
Bonatti, C. and Crovisier, S., ‘Récurrence et généricité’, Invent. Math. 158 (2004), 33–104.CrossRefGoogle Scholar
Doering, C., ‘Persistently transitive vector fields on three manifolds, dynamical systems and bifurcation theory’, Pitman Res. Notes Math. Ser. 160 (1987), 59–89.Google Scholar
Guchenheimer, J., ‘A strange, strange attractor’, in: The Hopf Bifurcation and its Applications, Applied Mathematical Sciences, 19 (ed. Marsden, J. E. and McCracken, M.) (Springer, New York, 1976), 368–381.CrossRefGoogle Scholar
Hayashi, S., ‘Diffeomorphisms in ${\mathbf{\mathcal{F}}}^1(M)$ satisfy Axiom A’, Ergod. Th. & Dynam. Sys. 12 (1992), 233–253.CrossRefGoogle Scholar
Hayashi, S., ‘Connecting invariant manifolds and the solution of the ${C}^1$stability conjectures for flows’, Ann. Math. 145 (1997), 81–137.CrossRefGoogle Scholar
Hayashi, S., ‘Corrections to: “Connecting invariant manifolds and the solution of the ${C}^1$stability conjectures for flows”’, Ann. Math. 150 (1999), 353–356.Google Scholar
Lee, K. and Lee, M., ‘Stably inverse shadowable transitive sets with dominated splittings’, Proc. Amer. Math. Soc. 140 (2012), 217–226.CrossRefGoogle Scholar
Lee, K. and Lee, M., ‘Shadowable chain recurrence classes for generic diffeomorphisms’, Taiwanese J. Math. 20 (2016), 399–409.CrossRefGoogle Scholar
Lee, K., Moriyasu, K. and Sakai, K., ‘$C^1$-stable shadowing diffeomorphisms’, Discrete Contin. Dyn. Syst. 22 (2008), 683–697.CrossRefGoogle Scholar
Lee, K. and Sakai, K., ‘Structural stability of vector fields with shadowing’, J. Differential Equations 232 (2007), 303–313.CrossRefGoogle Scholar
Lee, K., Tien, L. H. and Wen, X., ‘Robustly shadowable chain components of $C^1$-vector fields’, J. Korean Math. Soc. 51 (2014), 17–53.CrossRefGoogle Scholar
Lee, M., ‘$C^1$-stable inverse shadowing chain components for generic diffeomorphisms’, Commun. Korean Math. Soc. 24 (2009), 127–144.CrossRefGoogle Scholar
Lee, M., ‘Stably average shadowable homoclinic classes’, Nonlinear Anal. 74 (2011), 689–694.CrossRefGoogle Scholar
Lee, M., ‘Stably asymptotic average shadowing property and dominated splitting’, Adv. Difference Equ. 2012 (2012), 1–6.CrossRefGoogle Scholar
Lee, M., ‘Robustly chain transitive sets with orbital shadowing diffeomorphisms’, Dyn. Syst. 27 (2012), 507–514.CrossRefGoogle Scholar
Lee, M., ‘Usual limit shadowable homoclinic classes of generic diffeomorphisms’, Adv. Difference Equ. 2012 (2012), 1–8.CrossRefGoogle Scholar
Lee, M., ‘Chain components with $C^1$-stably orbital shadowing’, Adv. Difference Equ. 2013 (2013), 1–12.CrossRefGoogle Scholar
Lee, M., ‘The ergodic shadowing property and homoclinic classes’, J. Inequal. Appl. 2014 (2014), 1–10.CrossRefGoogle Scholar
Lee, M., ‘Locally maximal homoclinic classes for generic diffeomorphisms’, Balkan J. Geom. Appl. 22 (2017), 44–49.Google Scholar
Lee, M. and Lee, S., ‘Generic diffeomorphisms with robustly transitive sets’, Commun. Korean Math. Soc. 28 (2013), 581–587.CrossRefGoogle Scholar
Lee, M. and Lu, G., ‘Limit weak shadowable transitive sets of $C^1$-generic diffeomorphisms’, Commun. Korean Math. Soc. 27 (2012), 613–619.CrossRefGoogle Scholar
Lee, M. and Park, J., ‘Chain components with stably limit shadowing property are hyperbolic’, Adv. Difference Equ. 2014 (2014), 1–11.CrossRefGoogle Scholar
Lee, M. and Wen, X., ‘Diffeomorphisms with $C^1$-stably average shadowing’, Acta Math. Sin. (Engl. Ser.) 29 (2013), 85–92.CrossRefGoogle Scholar
Liao, S. T., ‘Obstruction sets II’, Acta Sci. Natur. Univ. Pekinensis 2 (1981), 9–30.Google Scholar
Mañé, R., ‘An ergodic closing lemma’, Ann. Math. 116 (1982), 503–540.CrossRefGoogle Scholar
Moriyasu, K., Sakai, K. and Sumi, N., ‘Vector fields with topological stability’, Trans. Amer. Math. Soc. 353 (2001), 3391–3408.CrossRefGoogle Scholar
Vivier, T., ‘Projective hyperbolicity and fixed points’, Ergod. Th. & Dynam. Sys. 26 (2006), 923–936.CrossRefGoogle Scholar
Wen, L., ‘On the $C^1$-stability conjecture for flows’, J. Differential Equations 129 (1996), 334–357.CrossRefGoogle Scholar