Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T14:19:13.319Z Has data issue: false hasContentIssue false
  • English
  • Français

Cesàro kernels on classical groups

Part of: Abstract harmonic analysis Lie groups

Published online by Cambridge University Press:  09 April 2009

Dashan Fan
Dashan Fan
Affiliation:
Department of Mathematical Sciences University of Wisconsin-MilwaukeeMilwaukee, WI 53201USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the Cesàro operator 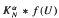on the classical group G and give a necessary and sufficient condition on the index α = α(G) for which the operator 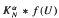is convergent to f(U) for any continuous function f as N → ∞. The result in this paper solves a question posed by Gong in the book Harmonic analysis on classical groups.

Keywords

Fourier seriesCesàro meansclassical groupLebesgue constant.

MSC classification

Secondary: 43A55: Summability methods on groups, semigroups, etc. 43A50: Convergence of Fourier series and of inverse transforms 43A80: Analysis on other specific Lie groups 22E20: General properties and structure of other Lie groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 63 , Issue 3 , December 1997 , pp. 364 - 389
Copyright
Copyright © Australian Mathematical Society 1997

References

[B]Boerner, H., Representations of groups (North-Holland Publishing Co., Amsterdam, 1970).Google Scholar
[C]Cartan, E., ‘Sur les domain bornés homogenes de l'espace de n variables’, Abh. Math. Sem. Univ. Hamburg 11 (1936), 106–162.Google Scholar
[CF]Chen, D. and Fan, D., ‘Cesàro kernels on symplectic groups’, unpublished manuscript, 1994.Google Scholar
[Cl]Clerc, J. L., ‘Sommes de Riesz et multiplicateurs sur un groupe Lie compact’, Ann. Inst. Fourier (Grenoble) 24 (1974), 149–172.CrossRefGoogle Scholar
[Fl]Fan, D., ‘Cesàro means of Fourier series on rotation groups’, Proc. Amer. Math. Soc. 123 (1995), 1105–1114.Google Scholar
[F2]Fan, D., ‘Salem theorem on compact Lie groups’, Chinese Ann. of Math. Ser. A 6 (1985), 397–410.Google Scholar
[F3]Fan, D., ‘Cesàro kernels on unitary groups’, unpublished manuscript, 1995.Google Scholar
[G]Gong, S., Harmonic analysis on classical groups (Springer, Berlin, 1991).Google Scholar
[GST1]Guilini, S., Soardi, P. M. and Travaglini, G., ‘A Cohen type inequality for compact Lie groups’, Proc. Amer. Math. Soc. 77 (1979), 359–364.CrossRefGoogle Scholar
[GST2]Guilini, S., Soardi, P. M. and Travaglini, G., ‘Norms of characters and Fourier series on compact Lie groups’, J. Funct. Anal. 46 (1982), 88–101.CrossRefGoogle Scholar
[H]Hua, L., Harmonic analysis of functions of several variables in the classical domains, Trans. Math. Monographs 6 (Amer. Math. Soc., Providence, 1963).CrossRefGoogle Scholar
[M]Meaney, C., ‘Unbounded Lebesgue constants on compact groups’, Monatsh. Math. 91 (1981), 119–129.CrossRefGoogle Scholar
[W]Weyl, H., The classical groups (Princeton Univ. Press, Princeton, 1939).Google Scholar
[Z]Zygmund, A., Trigonometric series, 2nd edition (Cambridge Univ. Press, Cambridge, 1968).Google Scholar