Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-16T17:09:15.658Z Has data issue: false hasContentIssue false
  • English
  • Français

Certain representation algebras

Published online by Cambridge University Press:  09 April 2009

S. B. Conlon
S. B. Conlon
Affiliation:
University of Sydney.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

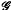Let Λ be the set of inequivalent representations of a finite group over a field 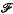. Λ is made the basis of an algebra 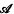over the complex numbers 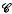, called the representation algebra, in which multiplication corresponds to the tensor product of representations and addition to direct sum. Green [5] has shown that if char 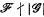(the non-modular case) or if 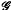is cyclic, then 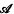is semi-simple, i.e. is a direct sum of copies of 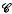. 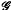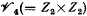Here we consider two modular, non-cyclic cases, viz, where is or 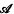4 (alternating group) and 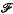is of characteristic 2.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 5 , Issue 1 , February 1965 , pp. 83 - 99
Copyright
Copyright © Australian Mathematical Society 1965

References

[1]Bašev, V. A., Representations of the group Z2 × Z2 in a field of characteristic 2, (Russian), Dokl. Akad. Nauk. SSSR 141 (1961), 1015—1018.Google Scholar
[2]Conlon, S. B., Twisted group algebras and their representations, This Journal 4 (1964), 152—173.Google Scholar
[3]Curtis, , Charles, W.; Reiner, Irving. Representation Theory of finite groups and associative algebras. Interscience, New York; 1962.Google Scholar
[4]Gantmacher, F. R., Applications of the theory of matrices. Interscience, New York, 1959.Google Scholar
[5]Green, J. A., The modular representation algebra of a finite group, Illinois J. Math. 6 (4) (1962) 607—619.CrossRefGoogle Scholar
[6]Heller, A.; Reiner I., Indecomposable representations, Illinois J. Math. 5 (1961), 314—323.Google Scholar
[7]Higman, D. G., Indecomposable representations at characteristic p. Duke Math. J. 21 (1954), 377—381.Google Scholar