Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-22T23:02:56.518Z Has data issue: false hasContentIssue false
  • English
  • Français

CAYLEY–ABELS GRAPHS AND INVARIANTS OF TOTALLY DISCONNECTED, LOCALLY COMPACT GROUPS

Part of: Noncompact transformation groups Graph theory Locally compact groups and their algebras Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  13 April 2022

ARNBJÖRG SOFFÍA ÁRNADÓTTIR Open the ORCID record for ARNBJÖRG SOFFÍA ÁRNADÓTTIR [Opens in a new window] ,
WALTRAUD LEDERLE Open the ORCID record for WALTRAUD LEDERLE [Opens in a new window]  and
RÖGNVALDUR G. MÖLLER Open the ORCID record for RÖGNVALDUR G. MÖLLER [Opens in a new window]
ARNBJÖRG SOFFÍA ÁRNADÓTTIR
Affiliation:
Department of Combinatorics and Optimization, University of Waterloo, 200 University Avenue West, Waterloo, Ontario, Canada N2L 3G1 e-mail: [email protected]
WALTRAUD LEDERLE
Affiliation:
Institut de Recherche en Mathématique et Physique, UCLouvain, Chemin du Cyclotron 2, 1348 Louvain-la-Neuve, Belgium e-mail: [email protected]
RÖGNVALDUR G. MÖLLER*
Affiliation:
Science Institute, University of Iceland, IS-107 Reykjavík, Iceland
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A connected, locally finite graph 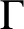$\Gamma $ is a Cayley–Abels graph for a totally disconnected, locally compact group G if G acts vertex-transitively on 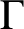$\Gamma $ with compact, open vertex stabilizers. Define the minimal degree of G as the minimal degree of a Cayley–Abels graph of G. We relate the minimal degree in various ways to the modular function, the scale function and the structure of compact open subgroups. As an application, we prove that if 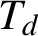$T_{d}$ denotes the d-regular tree, then the minimal degree of 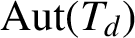$\mathrm{Aut}(T_{d})$ is d for all 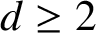$d\geq 2$ .

Keywords

totally disconnected locally compact groupsCayley–Abels graphsmodular functionscale functiongroups acting on trees

MSC classification

Primary: 22F50: Groups as automorphisms of other structures
Secondary: 05C25: Graphs and abstract algebra (groups, rings, fields, etc.) 20E08: Groups acting on trees 22D05: General properties and structure of locally compact groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 114 , Issue 2 , April 2023 , pp. 145 - 177
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by George Willis

The second named author was supported by Early Postdoc. Mobility scholarship No. 175106 from the Swiss National Science Foundation. Part of this work was done when she was visiting the University of Newcastle with the International Visitor Program of the Sydney Mathematical Research Institute.

References

Abels, H., ‘Specker-Kompaktifizierungen von lokal kompakten topologischen Gruppen’, Math. Z. 135 (1974), 325–361.CrossRefGoogle Scholar
Árnadóttir, A. S., Group Actions on Infinite Digraphs and the Suborbit Function, Master’s thesis, University of Iceland, 2016. https://skemman.is/handle/1946/26222.Google Scholar
Árnadóttir, A. S., Lederle, W. and Möller, R. G., ‘Trivalent vertex-transitive graphs with infinite vertex-stabilizers’, Preprint, 2021, arXiv:2101.04064.Google Scholar
Bass, H. and Kulkarni, R., ‘Uniform tree lattices’, J. Amer. Math. Soc. 3(4) (1990), 843–902.CrossRefGoogle Scholar
Bass, H. and Lubotzky, A., ‘Rigidity of group actions on locally finite trees’, Proc. Lond. Math. Soc. (3) 69(3) (1994), 541–575.CrossRefGoogle Scholar
Bhattacharjee, M. and Macpherson, D., ‘Strange permutation representations of free groups’, J. Aust. Math. Soc. 74(2) (2003), 267–285.CrossRefGoogle Scholar
Bywaters, T. P., Glöckner, H. and Tornier, S., ‘Contraction groups and passage to subgroups and quotients for endomorphisms of totally disconnected locally compact groups’, Israel J. Math. 227(2) (2018), 691–752.CrossRefGoogle Scholar
Caprace, P.-E., Reid, C. D. and Willis, G. A., ‘Locally normal subgroups of totally disconnected groups. Part II: Compactly generated simple groups’, Forum Math. Sigma 5 (2017), e12.CrossRefGoogle Scholar
Cornulier, Y., ‘Locally compact wreath products’, J. Aust. Math. Soc. 107(1) (2019), 26–52.CrossRefGoogle Scholar
Evans, D. M., ‘An infinite highly arc-transitive digraph’, European J. Combin. 18(3) (1997), 281–286.CrossRefGoogle Scholar
Garrido, A., Glasner, Y. and Tornier, S., ‘Automorphism groups of trees: generalities and prescribed local actions’, in: New Directions in Locally Compact Groups, London Mathematical Society Lecture Note Series, 447 (eds. Caprace, P.-E. and Monod, N.) (Cambridge University Press, Cambridge, 2018), 92–116.CrossRefGoogle Scholar
Glöckner, H., ‘Locally compact groups built up from $p$ -adic Lie groups, for $p$ in a given set of primes’, J. Group Theory 9(4) (2006), 427–454.CrossRefGoogle Scholar
Glöckner, H. and Willis, G. A., ‘Uniscalar $p$ -adic Lie groups’, Forum Math. 13(3) (2001), 413–421.CrossRefGoogle Scholar
Hammack, R., Imrich, W. and Klavžar, S., Handbook of Product Graphs, 2nd edn, Discrete Mathematics and Its Applications (CRC Press, Boca Raton, FL, 2011), with a foreword by Peter Winkler.CrossRefGoogle Scholar
Hopf, H., ‘Enden offener Räume und unendliche diskontinuierliche Gruppen’, Comment. Math. Helv. 16 (1944), 81–100.CrossRefGoogle Scholar
Jung, H. A. and Watkins, M. E., ‘Fragments and automorphisms of infinite graphs’, European J. Combin. 5(2) (1984), 149–162.CrossRefGoogle Scholar
Kepert, A. G. and Willis, G. A., ‘Scale functions and tree ends’, J. Aust. Math. Soc. 70(2) (2001), 273–292.CrossRefGoogle Scholar
Klopsch, B. and Vannacci, M., ‘Embedding properties of hereditarily just infinite profinite wreath products’, J. Algebra 476 (2017), 297–310.CrossRefGoogle Scholar
Krön, B. and Möller, R. G., ‘Analogues of Cayley graphs for topological groups’, Math. Z. 258(3) (2008), 637–675.CrossRefGoogle Scholar
Mazurov, V. D., ‘The minimal permutation representation of the Thompson simple group’, Algebra Logika 27(5) (1988), 562–580.CrossRefGoogle Scholar
Möller, R. G., ‘Ends of graphs. II’, Math. Proc. Cambridge Philos. Soc. 111(3) (1992), 455–460.CrossRefGoogle Scholar
Möller, R. G., ‘Structure theory of totally disconnected locally compact groups via graphs and permutations’, Canad. J. Math. 54(4) (2002), 795–827.CrossRefGoogle Scholar
Möller, R. G., ‘Graphs, permutations and topological groups’, Preprint, 2010, arXiv:1008.3062.Google Scholar
Möller, R. G. and Seifter, N., ‘Digraphical regular representations of infinite finitely generated groups’, European J. Combin. 19(5) (1998), 597–602.CrossRefGoogle Scholar
Nebbia, C., ‘Minimally almost periodic totally disconnected groups’, Proc. Amer. Math. Soc. 128(2) (2000), 347–351.CrossRefGoogle Scholar
Praeger, C. E., ‘On homomorphic images of edge transitive directed graphs’, Australas. J. Combin. 3 (1991), 207–210.Google Scholar
Reid, C., ‘Uniqueness of composition series for profinite groups’, version: 2014-02-19, accessed: 2021-03-02, MathOverflow. https://mathoverflow.net/q/158004.Google Scholar
Sabidussi, G., ‘Vertex-transitive graphs’, Monatsh. Math. 68 (1964), 426–438.CrossRefGoogle Scholar
Schlichting, G., ‘Polynomidentitäten und Permutationsdarstellungen lokalkompakter Gruppen’, Invent. Math. 55(2) (1979), 97–106.CrossRefGoogle Scholar
Schlichting, G., ‘Operationen mit periodischen Stabilisatoren’, Arch. Math. (Basel) 34(2) (1980), 97–99.CrossRefGoogle Scholar
Serre, J.-P., Trees, Springer Monographs in Mathematics, translated from the French original by John Stillwell, corrected 2nd printing of the 1980 English translation (Springer-Verlag, Berlin, 2003).Google Scholar
Tits, J., ‘Sur le groupe des automorphismes d’un arbre’, in: Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham) (eds. Haefliger, A. and Narasimhan, R.) (Springer, New York, 1970), 188–211.CrossRefGoogle Scholar
Trofimov, V. I., ‘Groups of automorphisms of graphs as topological groups’, Mat. Zametki 38(3) (1985), 378–385.Google Scholar
Trofimov, V. I., ‘Vertex stabilizers of graphs and tracks. I’, European J. Combin. 28(2) (2007), 613–640.CrossRefGoogle Scholar
van Dantzig, D., ‘Zur topologischen Algebra. III. Brouwersche und Cantorsche Gruppen’, Compos. Math. 3 (1936), 408–426.Google Scholar
Wall, C. T. C., ‘Poincaré complexes. I,’ Ann. of Math. (2) 86 (1967), 213–245.CrossRefGoogle Scholar
Willis, G. A., ‘The structure of totally disconnected, locally compact groups’, Math. Ann. 300(2) (1994), 341–363.CrossRefGoogle Scholar
Willis, G. A., ‘Further properties of the scale function on a totally disconnected group’, J. Algebra 237(1) (2001), 142–164.CrossRefGoogle Scholar
Wilson, J. S., Profinite Groups, London Mathematical Society Monographs. N. S., 19 (Clarendon Press, Oxford, 1998).Google Scholar
Woess, W., ‘Topological groups and infinite graphs’, Discrete Math. 95(1–3) (1991), 373–384.CrossRefGoogle Scholar