Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T07:17:51.111Z Has data issue: false hasContentIssue false
  • English
  • Français

CAYLEY SUM GRAPHS OF IDEALS OF A COMMUTATIVE RING

Part of: Graph theory General commutative ring theory

Published online by Cambridge University Press:  16 June 2014

M. AFKHAMI ,
Z. BARATI ,
K. KHASHYARMANESH  and
N. PAKNEJAD
M. AFKHAMI
Affiliation:
Department of Mathematics, University of Neyshabur, PO Box 91136-899, Neyshabur, Iran email [email protected]
Z. BARATI
Affiliation:
Department of Mathematics, Kosar University of Bojnord, PO Box 9415615458, Bojnord, Iran email [email protected]
K. KHASHYARMANESH*
Affiliation:
Department of Pure Mathematics, Ferdowsi University of Mashhad, PO Box 1159-91775, Mashhad, Iran email [email protected]
N. PAKNEJAD
Affiliation:
Department of Pure Mathematics, Ferdowsi University of Mashhad, PO Box 1159-91775, Mashhad, Iran email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 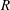$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}R$ be a commutative ring, 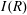$I(R)$ be the set of all ideals of 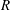$R$ and 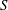$S$ be a subset of 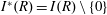$I^*(R)=I(R)\setminus \{0\}$. We define a Cayley sum digraph of ideals of 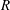$R$, denoted by 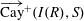$\overrightarrow{\mathrm{Cay}}^+ (I(R),S)$, as a directed graph whose vertex set is the set 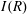$I(R)$ and, for every two distinct vertices 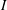$I$ and 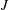$J$, there is an arc from 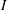$I$ to 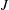$J$, denoted by $I\longrightarrow J$, whenever 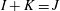$I+K=J$, for some ideal 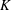$K $ in 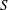$S$. Also, the Cayley sum graph 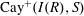$ \mathrm{Cay}^+ (I(R), S)$ is an undirected graph whose vertex set is the set 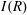$I(R)$ and two distinct vertices 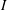$I$ and 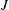$J$ are adjacent whenever 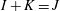$I+K=J$ or 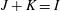$J+K=I$, for some ideal 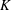$K $ in 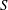$ S$. In this paper, we study some basic properties of the graphs 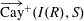$\overrightarrow{\mathrm{Cay}}^+ (I(R),S)$ and 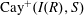$ \mathrm{Cay}^+ (I(R), S)$ such as connectivity, girth and clique number. Moreover, we investigate the planarity, outerplanarity and ring graph of 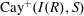$ \mathrm{Cay}^+ (I(R), S)$ and also we provide some characterization for rings $R$ whose Cayley sum graphs have genus one.

Keywords

Cayley sum graphplanar graphclique numbergenus number

MSC classification

Secondary: 05C10: Planar graphs; geometric and topological aspects of graph theory 05C69: Dominating sets, independent sets, cliques 13A15: Ideals; multiplicative ideal theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 96 , Issue 3 , June 2014 , pp. 289 - 302
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Afkhami, M., Ahmadi, M. R., Jahani-Nezhad, R. and Khashyarmanesh, K., ‘Cayley graphs of ideals in a commutative ring’, Bull. Malays. Math. Sci. Soc. to appear.Google Scholar
Afkhami, M., Karimi, M. and Khashyarmanesh, K., ‘On the regular digraph of ideals of commutative rings’, Bull. Aust. Math. Soc. 88 (2013), 177–189.CrossRefGoogle Scholar
Afkhami, M., Khashyarmanesh, K. and Nafar, Kh., ‘Generalized Cayley graphs associated to commutative rings’, Linear Algebra Appl. 437 (2012), 1040–1049.Google Scholar
Akbari, S., Maimani, H. R. and Yassemi, S., ‘When a zero-divisor graph is planar or a complete r-partite graph’, J. Algebra 270 (2003), 169–180.CrossRefGoogle Scholar
Anderson, D. D. and Naseer, M., ‘Beck’s coloring of a commutative ring’, J. Algebra 159 (1993), 500–514.Google Scholar
Anderson, D. F. and Badawi, A., ‘On the zero-divisor graph of a ring’, Comm. Algebra 36 (2008), 3073–3092.CrossRefGoogle Scholar
Anderson, D. F. and Livingston, P. S., ‘The zero-divisor graph of a commutative ring’, J. Algebra 217 (1999), 434–447.Google Scholar
Beck, I., ‘Coloring of commutative rings’, J. Algebra 116 (1998), 208–226.Google Scholar
Bondy, J. A. and Murty, U. S. R., Graph Theory with Applications (American Elsevier, New York, 1976).Google Scholar
Chakrabarty, I., Ghosh, S., Mukherjee, T. K. and Sen, M. K., ‘Intersection graphs of ideals of rings’, Discrete Math. 309 (2009), 5381–5392.Google Scholar
Gitler, I., Reyes, E. and Villarreal, R. H., ‘Ring graphs and complete intersection toric ideals’, Discrete Math. 310 (2010), 430–441.CrossRefGoogle Scholar
Kelarev, A. V., ‘Directed graphs and nilpotent rings’, J. Aust. Math. Soc. 65 (1998), 326–332.CrossRefGoogle Scholar
Kelarev, A. V., ‘On undirected Cayley graphs’, Australas. J. Combin. 25 (2002), 73–78.Google Scholar
Kelarev, A. V., Ring Constructions and Applications (World Scientific, River Edge, NJ, 2002).Google Scholar
Kelarev, A. V., Graph Algebras and Automata (Marcel Dekker, New York, 2003).Google Scholar
Kelarev, A. V., ‘Labelled Cayley graphs and minimal automata’, Australas. J. Combin. 30 (2004), 95–101.Google Scholar
Kelarev, A. V., ‘On Cayley graphs of inverse semigroups’, Semigroup Forum 72 (2006), 411–418.CrossRefGoogle Scholar
Kelarev, A. V. and Praeger, C. E., ‘On transitive Cayley graphs of groups and semigroups’, European J. Combin. 24 (2003), 59–72.Google Scholar
Kelarev, A. V. and Quinn, S. J., ‘A combinatorial property and power graphs of groups’, Contrib. Gen. Algebra 12 (2000), 229–235.Google Scholar
Kelarev, A. V. and Quinn, S. J., ‘Directed graphs and combinatorial properties of semigroups’, J. Algebra 251 (2002), 16–26.Google Scholar
Kelarev, A. V., Ryan, J. and Yearwood, J., ‘Cayley graphs as classifiers for data mining: the influence of asymmetries’, Discrete Math. 309 (2009), 5360–5369.Google Scholar
Nikmehr, M. J. and Shaveisi, F., ‘The regular digraph of ideals of a commutative ring’, Acta Math. Hungar. 134 (2012), 516–528.CrossRefGoogle Scholar
White, A. T., ‘The genus of the Cartesian product of two graphs’, J. Combin. Theory Ser. B 11 (1971), 89–94.Google Scholar
White, A. T., Graphs, Groups and Surfaces (North-Holland, Amsterdam, 1973).Google Scholar