Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-05T00:43:23.078Z Has data issue: false hasContentIssue false
  • English
  • Français

Categories of certain minimal topological spaces

Published online by Cambridge University Press:  09 April 2009

Manuel P. Berri
Manuel P. Berri
Affiliation:
Tulane University of Louisiana
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The main purpose of this paper is to discuss the categories of the minimal topological spaces investigated in [1], [2], [7], and [8]. After these results are given, an application will be made to answer the following question: If is the lattice of topologies on a set X and 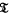is a Hausdorff (or regular, or completely regular, or normal, or locally compact) topology does there always exist a minimal Hausdorff (or minimal regular, or minimal completely regular, or minimal normal, or minimal locally compact) topology weaker than ?

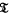Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 4 , Issue 1 , February 1964 , pp. 78 - 82
Copyright
Copyright © Australian Mathematical Society 1964

References

[1]Berri, Manuel P., Minimal Topological Spaces, Trans. Amer. Math. Soc. 1 (1963), 97–105.Google Scholar
[2]Berri, Manuel P. and Sorgenfrey, R. H., Minimal Regular Spaces, Proc. Amer. Math. Soc. 3 (1963), 454–458.CrossRefGoogle Scholar
[3]Bourbaki, N., Eléments de Mathématique (le partie). Livre III: Topologie Générale;. Chapitres I-II. (Actualités Sci. Ind. 858–1142, Hermann, Paris, 1951).Google Scholar
[4]Bourbaki, N., Eléments de Mathématique (le partie). Livre III: Topologie Générale. Chapitres IX. (Actualités Sci. Ind. 1045, Hermann, Paris, 1948).Google Scholar
[5]Bourbaki, N., Espaces Minimaux et Espaces Complètement Séparés, 215–218.Google Scholar
[6]Kelley, J. L., General Topology (Van Nostrand, New York, 1955).Google Scholar
[7]Ramanathan, A., Maximal Hausdorff Spaces, Proc. Indian Acad. Sci. Sect. A 26 (1947), 31–42.CrossRefGoogle Scholar
[8]Smythe, N. and Wilkins, C. A., Minimal Hausdorff and Maximal Compact Spaces, this Journal 3 (1963), 167–171.Google Scholar
[9]Urysohn, P., Über die Mächtigkeit der zusammenhangenden Mengen, Math. Ann. 94 (1925), 262–295.CrossRefGoogle Scholar