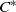Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T14:25:40.417Z Has data issue: false hasContentIssue false
  • English
  • Français

${C}^{\ast } $-ALGEBRAS ASSOCIATED WITH LAMBDA-SYNCHRONIZING SUBSHIFTS AND FLOW EQUIVALENCE

Part of: Selfadjoint operator algebras Topological dynamics

Published online by Cambridge University Press:  07 August 2013

KENGO MATSUMOTO
KENGO MATSUMOTO*
Affiliation:
Department of Mathematics, Joetsu University of Education, Joetsu 943-8512, Japan
*
[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The class of 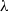$\lambda $-synchronizing subshifts generalizes the class of irreducible sofic shifts. A 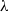$\lambda $-synchronizing subshift can be presented by a certain 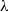$\lambda $-graph system, called the 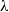$\lambda $-synchronizing 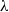$\lambda $-graph system. The 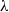$\lambda $-synchronizing 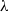$\lambda $-graph system of a 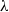$\lambda $-synchronizing subshift can be regarded as an analogue of the Fischer cover of an irreducible sofic shift. We will study algebraic structure of the 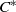${C}^{\ast } $-algebra associated with a 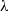$\lambda $-synchronizing 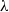$\lambda $-graph system and prove that the stable isomorphism class of the 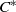${C}^{\ast } $-algebra with its Cartan subalgebra is invariant under flow equivalence of 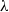$\lambda $-synchronizing subshifts.

Keywords

subshiftsC∗-algebrasλ-graph systemsflow equivalenceK-groupsBowen–Franks groupsλ-synchronization

MSC classification

Secondary: 46L35: Classifications of $C^*$-algebras 37B10: Symbolic dynamics 46L80: $K$-theory and operator algebras (including cyclic theory)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 95 , Issue 2 , October 2013 , pp. 241 - 265
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Bates, T., Eilers, S. and Pask, D., ‘Reducibility of covers of AFT shifts’, Israel J. Math. 185 (2011), 207–234.CrossRefGoogle Scholar
Bates, T. and Pask, D., ‘The ${C}^{\ast } $-algebras of labelled graphs’, J. Operator Theory 57 (2007), 207–226.Google Scholar
Blanchard, F. and Hansel, G., ‘Systèmes codés’, Theor. Comput. Sci. 44 (1986), 17–49.CrossRefGoogle Scholar
Bowen, R. and Franks, J., ‘Homology for zero-dimensional nonwandering sets’, Ann. of Math. (2) 106 (1977), 73–92.CrossRefGoogle Scholar
Brown, L. G., ‘Stable isomorphism of hereditary subalgebras of ${C}^{\ast } $-algebras’, Pacific. J. Math. 71 (1977), 335–348.CrossRefGoogle Scholar
Carlesen, T. M. and Matsumoto, K., ‘Some remarks on the ${C}^{\ast } $-algebras associated with subshifts’, Math. Scand. 95 (2004), 145–160.CrossRefGoogle Scholar
Cuntz, J., ‘Simple ${C}^{\ast } $-algebras generated by isometries’, Commun. Math. Phys. 57 (1977), 173–185.CrossRefGoogle Scholar
Cuntz, J. and Krieger, W., ‘A class of ${C}^{\ast } $-algebras and topological Markov chains’, Invent. Math. 56 (1980), 251–268.CrossRefGoogle Scholar
Fischer, R., ‘Sofic systems and graphs’, Monatsh. Math. 80 (1975), 179–186.CrossRefGoogle Scholar
Franks, J., ‘Flow equivalence of subshifts of finite type’, Ergodic Theory Dynam. Systems 4 (1984), 53–66.CrossRefGoogle Scholar
Fujiwara, M. and Oshikawa, M., ‘Sofic shifts and flow equivalence’, Math. Rep. Kyushu Univ. 16 (1987), 17–27.Google Scholar
Hamachi, T., Inoue, K. and Krieger, W., ‘Subsystems of finite type and semigroup invariants of subshifts’, J. reine angew. Math. 632 (2009), 37–69.Google Scholar
Katayama, Y., Matsumoto, K. and Watatani, Y., ‘Simple ${C}^{\ast } $-algebras arising from $\beta $-expansion of real numbers’, Ergodic Theory Dynam. Systems 18 (1998), 937–962.CrossRefGoogle Scholar
Kirchberg, E., ‘The classification of purely infinite ${C}^{\ast } $-algebras using Kasparov’s theory’, Preprint, 1994.Google Scholar
Kirchberg, E. and Phillips, N. C., ‘Embedding of exact ${C}^{\ast } $-algebras in the Cuntz algebra ${ \mathcal{O} }_{2} $’, J. reine angew. Math. 525 (2000), 17–53.CrossRefGoogle Scholar
Kitchens, B. P., Symbolic Dynamics (Springer, Berlin, 1998).CrossRefGoogle Scholar
Krieger, W., ‘On the uniqueness of the equilibrium state’, Math. Systems Theory 8 (1974), 97–104.CrossRefGoogle Scholar
Krieger, W., ‘On sofic systems I’, Israel J. Math. 48 (1984), 305–330.CrossRefGoogle Scholar
Krieger, W., ‘On sofic systems II’, Israel J. Math. 60 (1987), 167–176.CrossRefGoogle Scholar
Krieger, W., ‘On $g$-functions for subshifts’, in: Dynamics and Stochastics, Institute of Mathematical Statistics Lecture Notes—Monograph Series, 48 (Institute of Mathematical Statistics, Beachwood, OH, 2006), 306–316.Google Scholar
Krieger, W., ‘On subshifts and semigroups’, Bull. London Math. 38 (2006), 617–624.CrossRefGoogle Scholar
Krieger, W. and Matsumoto, K., ‘A lambda-graph system for the Dyck shift and its $K$-groups’, Doc. Math. 8 (2003), 79–96.CrossRefGoogle Scholar
Krieger, W. and Matsumoto, K., ‘A notion of synchronization of symbolic dynamics and a class of ${C}^{\ast } $-algebras’, Acta Appl. Math., to appear, arXiv:1105.4393.Google Scholar
Lind, D. and Marcus, B., An Introduction to Symbolic Dynamics and Coding (Cambridge University Press, Cambridge, 1995).CrossRefGoogle Scholar
Matsumoto, K., ‘On ${C}^{\ast } $-algebras associated with subshifts’, Internat. J. Math. 8 (1997), 357–374.CrossRefGoogle Scholar
Matsumoto, K., ‘A simple ${C}^{\ast } $-algebra arising from a certain subshift’, J. Operator Theory 42 (1999), 351–370.Google Scholar
Matsumoto, K., ‘Presentations of subshifts and their topological conjugacy invariants’, Doc. Math. 4 (1999), 285–340.CrossRefGoogle Scholar
Matsumoto, K., ‘Bowen–Franks groups for subshifts and Ext-groups for ${C}^{\ast } $-algebras’, K-Theory 23 (2001), 67–104.CrossRefGoogle Scholar
Matsumoto, K., ‘Bowen–Franks groups as an invariant for flow equivalence of subshifts’, Ergodic Theory Dynam. Systems 21 (2001), 1831–1842.CrossRefGoogle Scholar
Matsumoto, K., ‘${C}^{\ast } $-algebras associated with presentations of subshifts’, Doc. Math. 7 (2002), 1–30.CrossRefGoogle Scholar
Matsumoto, K., ‘Strong shift equivalence of symbolic matrix systems and Morita equivalence of ${C}^{\ast } $-algebras’, Ergodic Theory Dynam. Systems 24 (2004), 199–215.CrossRefGoogle Scholar
Matsumoto, K., ‘A simple purely infinite ${C}^{\ast } $-algebra associated with a lambda-graph system of Motzkin shift’, Math. Z. 248 (2004), 369–394.CrossRefGoogle Scholar
Matsumoto, K., ‘Construction and pure infiniteness of ${C}^{\ast } $-algebras associated with lambda-graph systems’, Math. Scand. 97 (2005), 73–88.CrossRefGoogle Scholar
Matsumoto, K., ‘On the simple ${C}^{\ast } $-algebras arising from Dyck systems’, J. Operator Theory 58 (2007), 205–226.Google Scholar
Matsumoto, K., ‘${C}^{\ast } $-algebras arising from Dyck systems of topological Markov chains’, Math. Scand. 109 (2011), 31–54.CrossRefGoogle Scholar
Matsumoto, K., ‘A certain synchronizing property of subshifts and flow equivalence’, Israel J. Math., to appear, arXiv:1105.3249.Google Scholar
Parry, W. and Sullivan, D., ‘A topological invariant for flows on one-dimensional spaces’, Topology 14 (1975), 297–299.CrossRefGoogle Scholar
Phillips, N. C., ‘A classification theorem for nuclear purely infinite simple ${C}^{\ast } $-algebras’, Doc. Math. 5 (2000), 49–114.CrossRefGoogle Scholar
Rosenberg, J. and Schochet, C., ‘The Künneth theorem and the universal coefficient theorem for Kasparov’s generalized $K$-functor’, Duke Math. J. 55 (1987), 431–474.CrossRefGoogle Scholar
Weiss, B., ‘Subshifts of finite type and sofic systems’, Monats. Math. 77 (1973), 462–474.CrossRefGoogle Scholar