Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T13:34:20.940Z Has data issue: false hasContentIssue false
  • English
  • Français

Cartan subalgebras of regular extensions of von Neumann algebras

Part of: Locally compact groups and their algebras Selfadjoint operator algebras

Published online by Cambridge University Press:  09 April 2009

Colin E. Sutherland
Colin E. Sutherland
Affiliation:
Mathematics Department The University of New South WalesP.O. Box 1 Kensington, N.S.W. 2033, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We analyse the structure of a regular extension ℳ ⋊ γ, υQ of a von Neumann algebra ℳ by an action (modulo inner automorphisms) γ of a discrete group Q, and a nonabelian 2-cycle υ for γ, under the assumption that the “action” γ of Q is cocycle conjugate to an “action”, α which leaves globally invariant a cartan subalgebra 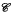of ℳ. we show that ℳ ⋊ γ, υQ is isomorphic with the algebra of the left regular projective representation of a certain discrete, non-principal groupoid ℜ V Q determined by the action of Q on the given cartan subalgebrs, where ℜ is the Takesaki relation associated to the pair (ℳ, 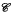) we apply this description to give a decomposition of the regular representation of a group G into irreducibles, where G is a split extension of a type I group K by an abelian group Q, and work out the details of the author's earlier abstract plancherel theorem in the case when K is abelian.

MSC classification

Secondary: 46L10: General theory of von Neumann algebras 22D25: $C^*$-algebras and $W^*$-algebras in relation to group representations
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 45 , Issue 2 , October 1988 , pp. 249 - 274
Copyright
Copyright © Australian Mathematical Society 1988

References

[1]Connes, A., Sur la theorie non-commutative de l'integration (Springer Lecture Notes in Math., No. 725).Google Scholar
[2]Connes, A., ‘Classification of injective factors: Cases II1, II∞ and IIIλ, λ ≠ 1, Ann. of Math. (2) 104 (1976), 73–115.CrossRefGoogle Scholar
[3]Connes, A., Feldman, J. and Weiss, B., ‘An amenable equivalence relation is generated by a single transformation’, Ergodic Theory Dynamical Systems 1 (1981), 431–450.CrossRefGoogle Scholar
[4]Dixmier, J., ‘Sur la représentation réguliere d' une groupe localement compact’, Ann. Sci. Ecole Norm. Sup 2 (1969), 423–436.CrossRefGoogle Scholar
[5]Dixmier, J., Les C*-algebres et leurs representations (Gauthier-villars, 2eme edition, Paris, 1968)Google Scholar
[6]Feldman, J. and Moore, C. C., ‘Ergodic equivalence relations, cohomology, and von neumann Algebra’, I and II, Trans. Amer. Math. Soc. 274 (1977), 289–324 and 325–359.CrossRefGoogle Scholar
[7]Green, P., ‘The local structure of twisted covariance algebras’, Acta Math. 140 (1978), 191–250.CrossRefGoogle Scholar
[8]Haagerup, U., ‘Standard forms of von neumann algebras’, Math. Scand. 37 (1975), 271–283.CrossRefGoogle Scholar
[9]Hahn, P., ‘Reconstruction of a factor from measures on Takesakis unitary equicalence relation’, J. Fund. Anal. 31 (1979), 263–271.CrossRefGoogle Scholar
[10]Jones, V. F. R. and Takesaki, M., ‘Actions of compact abelian groups on semifinite injective factors’, Acta Math. 153 (1984), 213–258.CrossRefGoogle Scholar
[11]Mackey, G. W., ‘Unitary representations of group extensions I’, Acta Math. 99 (1958), 265–311.CrossRefGoogle Scholar
[12]Ramsay, A., ‘Non-transitive quasi-orbits in Mackeys analysis of group extensions’, Acta. Math. 137 (1976), 17–48.CrossRefGoogle Scholar
[13]Sutherland, C., ‘Maximal abelian subalgebras of von Neumann algebras, and representations of equivalence relations’, Trans. Amer. Math. Soc. 280 (1983), 321–336.CrossRefGoogle Scholar
[14]Sutherland, C., ‘Cohomology and extensions of von Neumann algebras II’, Publ. Res. Inst. Math. Sci. 16 (1980), 135–174.CrossRefGoogle Scholar
[15]Sutherland, C., ‘Cartan Subalgebras, Transverese measures and non-type I Plancherel formulae’, J. Funct. Anal. 60 (1985), 281–308.CrossRefGoogle Scholar
[16]Sutherland, C., ‘A Borel parametrization of Polish groups’, Publ. Res. Inst. Math. Sci. 21 (1985), 1067–1086.CrossRefGoogle Scholar
[17]Sutherland, C. and Takesaki, M., ‘Actions of discrete amenable groups and groupoids on semifinite injective von Neumann algebra’, Publ. Res. Inst. Math. Sci. 21 (1985), 1087–1120.CrossRefGoogle Scholar
[18]Takesaki, M., ‘On the unitary equivalence relation among components of decompositions of representations of involutive Banach algebras, and the associated diagonal algebras’, Tohuku Math. J. 15 (1963), 365–393.Google Scholar
[19]Zimmer, R., ‘Hyperfinite factors and amenable ergodic actions’, Invent. Math. 41 (1977), 23–31.CrossRefGoogle Scholar