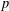Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zhao, Lin
and
Yan, Xingjie
2017.
A study of nonlinear elliptic problems involving supercritical and exponential growth in RN.
Mathematical Methods in the Applied Sciences,
Vol. 40,
Issue. 18,
p.
7162.
Ambrosio, Vincenzo
Mawhin, Jean
and
Bisci, Giovanni Molica
2018.
(Super)Critical nonlocal equations with periodic boundary conditions.
Selecta Mathematica,
Vol. 24,
Issue. 4,
p.
3723.
Ambrosio, Vincenzo
and
Essebei, Fares
2023.
Multiple solutions for double phase problems in Rn via Ricceri's principle.
Journal of Mathematical Analysis and Applications,
Vol. 528,
Issue. 1,
p.
127513.