Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T19:19:34.875Z Has data issue: false hasContentIssue false
  • English
  • Français

BOCHNER–RIESZ MEANS ON BLOCK-SOBOLEV SPACES IN COMPACT LIE GROUP

Part of: Harmonic analysis in several variables Abstract harmonic analysis

Published online by Cambridge University Press:  08 January 2020

JIECHENG CHEN ,
DASHAN FAN  and
FAYOU ZHAO
JIECHENG CHEN
Affiliation:
Department of Mathematics,Zhejiang Normal University, Jinhua 321000, PR China email [email protected]
DASHAN FAN
Affiliation:
Department of Mathematical Sciences,University of Wisconsin-Milwaukee, Milwaukee, WI 53201, USA Department of Mathematics,Zhejiang Normal University, Jinhua 321000, PR China email [email protected]
FAYOU ZHAO*
Affiliation:
Department of Mathematics,Shanghai University, Shanghai 200444, PR China email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

On a compact Lie group 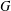$G$ of dimension $n$, we study the Bochner–Riesz mean 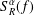$S_{R}^{\unicode[STIX]{x1D6FC}}(f)$ of the Fourier series for a function 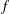$f$. At the critical index 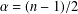$\unicode[STIX]{x1D6FC}=(n-1)/2$, we obtain the convergence rate for 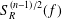$S_{R}^{(n-1)/2}(f)$ when 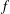$f$ is a function in the block-Sobolev space. The main theorems extend some known results on the $m$-torus 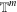$\mathbb{T}^{m}$.

Keywords

Bochner–Riesz meansblock spaceblock-Sobolev spacecompact Lie groupsFourier seriesmaximal operatoralmost everywhere convergence

MSC classification

Primary: 43A22: Homomorphisms and multipliers of function spaces on groups, semigroups, etc. 43A32: Other transforms and operators of Fourier type
Secondary: 42B25: Maximal functions, Littlewood-Paley theory 42B35: Function spaces arising in harmonic analysis
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 109 , Issue 2 , October 2020 , pp. 176 - 192
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research was supported by National Natural Science Foundation of China (grant nos. 11671363, 11871436, 11871108, 11971295) and Natural Science Foundation of Shanghai (no. 19ZR1417600).

References

Blank, B., ‘Nontangential maximal functions over compact Riemannian manifolds’, Proc. Amer. Math. Soc. 103 (1988), 999–1002.CrossRefGoogle Scholar
Bloom, W. R. and Xu, Z., ‘Approximation of H p-functions by Bochner–Riesz means on compact Lie groups’, Math. Z. 216 (1994), 131–145.CrossRefGoogle Scholar
Bochner, S., ‘Summation of multiple Fourier series by spherical means’, Trans. Amer. Math. Soc. 40 (1936), 175–207.CrossRefGoogle Scholar
Chen, X. and Fan, D., ‘On almost everywhere divergence of Bochner–Riesz means on compact Lie groups’, Math. Z. 289 (2018), 961–981.CrossRefGoogle Scholar
Clerc, J. L., ‘Sommes de Riesz et multiplicateurs sur un groupe de Lie compact’, Ann. Inst. Fourier (Grenoble) 24 (1974), 149–172.CrossRefGoogle Scholar
Coifman, R. and Weiss, G., ‘Extension of Hardy spaces and their use in analysis’, Bull. Amer. Math. Soc. 83 (1977), 569–645.CrossRefGoogle Scholar
Fan, D. and Zhao, F., ‘Block-Sobolev spaces and the rate of almost everywhere convergence of Bochner–Riesz means’, Constr. Approx. 45 (2017), 391–405.CrossRefGoogle Scholar
Fan, D. and Zhao, F., ‘Approximation properties of combination of multivariate averages on Hardy spaces’, J. Approx. Theory 223 (2017), 77–95.CrossRefGoogle Scholar
Fefferman, R., ‘A theory of entropy in Fourier analysis’, Adv. Math. 30 (1978), 171–201.CrossRefGoogle Scholar
Grafakos, L., Classical Fourier Analysis, 2nd edn, Graduate Texts in Mathematics, 249 (Springer, New York, 2008).Google Scholar
Lu, S., ‘Conjectures and problems on Bochner–Riesz means’, Front. Math. China 8 (2013), 1237–1251.CrossRefGoogle Scholar
Lu, S., Taibleson, M. H. and Weiss, G., ‘On the almost everywhere convergence of Bochner–Riesz means of multiple Fourier series’, in: Harmonic Analysis (Minneapolis, MN, 1981), Lecture Notes in Mathematics, 908 (Springer, Berlin–New York, 1982), 311–318.Google Scholar
Lu, S. and Wang, S., ‘Spaces generated by smooth blocks’, Constr. Approx. 8 (1992), 331–341.CrossRefGoogle Scholar
Stein, E. M., ‘An H 1  function with non-summable Fourier expansion’, in: Harmonic Analysis, Proc. Conf. Cortona, Italy, Lecture Notes in Mathematics, 992 (Springer-Verlag, Berlin–Heidelberg, 1983), 193–200.Google Scholar
Stein, E. M., Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals (Princeton University Press, Princeton, NJ, 1993).Google Scholar
Stein, E. M. and Weiss, G., Introduction to Fourier Analysis on Euclidean Spaces (Princeton University Press, Princeton, NJ, 1971).Google Scholar
Stein, E. M. and Weiss, N., ‘On the convergence of Poisson integrals’, Trans. Amer. Math. Soc. 140 (1969), 35–54.CrossRefGoogle Scholar
Strichartz, R., ‘Multipliers on fractional Sobolev spaces’, J. Math. Mech. 16 (1967), 1031–1060.Google Scholar
Strichartz, R., ‘H p Sobolev spaces’, Colloq. Math. LX/LXI (1990), 129–139.CrossRefGoogle Scholar
Taibleson, M. H. and Weiss, G., ‘Certain function spaces connected with almost everywhere convergence of Fourier series’, in: Conference on Harmonic Analysis in Honor of Antoni Zygmund, Vols I, II (Chicago, IL, 1981), Wadsworth Mathematical Series (Wadsworth, Belmont, CA, 1983), 95–113.Google Scholar
Xu, Z., ‘The generalized Abel means of H p functions on compact Lie groups’, Chin. Ann. Math. Ser. A 13(A) (1992), 101–110.Google Scholar
Zaloznik, A., ‘Function spaces generated by blocks associated with sphere, Lie groups and spaces of homogeneous type’, Trans. Amer. Math. Soc. 309 (1988), 139–164.CrossRefGoogle Scholar