Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T04:53:22.588Z Has data issue: false hasContentIssue false
  • English
  • Français

Bilinear forms and 2-dimensional cohomology

Part of: Lie groups

Published online by Cambridge University Press:  09 April 2009

Martin Moskowitz
Martin Moskowitz
Affiliation:
Graduate Centre, City University of New York, 33 West 42 Street, New York, New York 10036, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper calculates the central Borel 2 cocycles 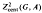for certain 2-step nilpotent Lie groups G with values in the injectives A of the category of 2nd countable locally compact abelian groups. The G's include, among others, all groups locally isomorphic to a Heisenberg group. The A's are direct sums of vector groups and (possibly infinite dimensional) tori, and in particular include R, T, and Cx. The main results are as follows.

(4.1) Every symmetric central 2 cocycle is trivial.

(4.2) Every central 2 cocycle is cohomologous with a skew symmetric bimultiplicative one (which is necessarily jointly continuous by [7]).

(4.3) The corresponding cohomology group H2cent (G, A) is calculated as the skew symmetric jointly continuous bimultiplicative maps modulo Homcont ([G, G]–, A).

These results generalize the case when G is a connected abelian Lie group and A = T, due to Kleppner [3]. Using standard facts of the cohomology of groups they can be interpreted as classifying all continuous central extensions (1) → A → E → G → (1) of the group G by the abelian group A. Finally some counterexamples are given to extending these results.

MSC classification

Secondary: 22E41: Continuous cohomology
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 41 , Issue 2 , October 1986 , pp. 165 - 179
Copyright
Copyright © Australian Mathematical Society 1986

References

[1]Phyllis, J. Cassidy, ‘Unipotent differential algebraic groups’, in Contributions to Algebra (a collection of papers dedicated to E. Kolchin), Academic Press (1977), pp. 83–115.Google Scholar
[2]Hochschild, G., The structure of Lie groups (Holden-Day, San Francisco, 1965).Google Scholar
[3]Kleppner, A., ‘Multipliers on Abelian groups’, Math. Ann. 158 (1965), 11–34.CrossRefGoogle Scholar
[4]Mackey, G. W., ‘Borel structures in groups and their duals’, Trans. Amer. Math. Soc. 85 (1957), 134–165.CrossRefGoogle Scholar
[5]Moore, C. C.; ‘Extensions and low dimensional cohomology theory of locally compact groups I’, Trans. Amer. Math. Soc. 113 (1964), 40–63.Google Scholar
[6]Moskowitz, M., ‘Homological algebra in locally compact abelian groups’, Trans. Amer. Math. Soc. 127 (1967), 361–409.CrossRefGoogle Scholar
[7]Moskowitz, M., ‘Uniform boundedness for non-abelian groups’, Proc. Cambridge Phil. Soc. 97 (1985), 107–110.CrossRefGoogle Scholar
[8]Ritt, J. F., ‘Associative differential operations’, Ann. of Math. 52 (1950), 756–765.CrossRefGoogle Scholar