No CrossRef data available.
Published online by Cambridge University Press: 09 April 2009
Let Bp be the bicyclic semigroup over P=G⋒[1,∞ where G is a subgroup of the multiplicative group of positive real numbers. If + is an addition which makes Bp, with its usual multiplication, into a semiring, then + is idempotent, and P is embedded as a sub-semiring in Bp and for each x in p, 1≦x+1≦x and 1≦1+x≦x. We show that any idempotent addition on P with these inequalities holding is max, min or trivial. The trivial addition on P extends trivially. If addition on P is min, then let 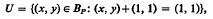 ,
, 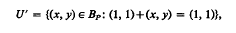 and
and 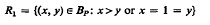 . We charactertize all additions on Bp in terms of U and U′; and, in particular If U=U′ is a proper subset of R1 we demonstrate a correspondence between all such additions and certain homomorphisms of G to (0,∞)
. We charactertize all additions on Bp in terms of U and U′; and, in particular If U=U′ is a proper subset of R1 we demonstrate a correspondence between all such additions and certain homomorphisms of G to (0,∞)
Subject classification (Amer. math. Soc. (MOS) 1970): primary 16 A 80; secondary 22 A 15.