Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T23:18:36.105Z Has data issue: false hasContentIssue false
  • English
  • Français

Balanced tournament designs with almost orthogonal resolutions

Part of: Designs and configurations

Published online by Cambridge University Press:  09 April 2009

E. R. Lamken  and
S. A. Vanstone
E. R. Lamken
Affiliation:
Department of Combinatorics and OptimizationUniversity of WaterlooWaterloo, Ontario N2L 3G1, Canada
S. A. Vanstone
Affiliation:
Department of Combinatorics and OptimizationUniversity of WaterlooWaterloo, Ontario N2L 3G1, Canada
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A balanced tournament design, BTD(n), defined on a 2n—set V is an arrangement of the (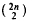) distinct unordered pairs of the elements of V into an n × 2n − 1 array such that (1) every element of V is contained in precisely one cell of each column, and (2) every element of V is contained in at most two cells of each row. In this paper, we investigate the existence of balanced tournament designs with a pair of almost orthogonal resolutions. These designs can be used to construct doubly resolvable (ν, 3, 2)- BIBD s and, in our smallest applications, have been used to construct previously unknown doubly resolvable (ν, 3, 2)- B I B D s.

MSC classification

Secondary: 05B30: Other designs, configurations
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 49 , Issue 2 , October 1990 , pp. 175 - 195
Copyright
Copyright © Australian Mathematical Society 1990

References

[1]Anderson, B. A., ‘Howell designs of type H(p − 1, p + 1)’, J. Combin. Theory Ser. A 24 (1978), 131–140.CrossRefGoogle Scholar
[2]Dinitz, J. H. and Stinson, D. R., ‘The construction and uses of frames’, Ars Combin. 10 (1980), 31–53.Google Scholar
[3]Dinitz, J. H. and Stinson, D. R., ‘MOLS with holes’, Discrete Math. 44 (1983), 145–154.CrossRefGoogle Scholar
[4]Hanani, H., ‘On balanced incomplete block designs with blocks having 5 elements’, J. Combin. Theory Ser. A 12 (1972), 184–201.CrossRefGoogle Scholar
[5]Hung, S. H. Y. and Mendelsohn, N. S., ‘On Howell designs’, J. Combin. Theory Ser. A 16 (1974), 174–198.CrossRefGoogle Scholar
[6]Lamken, E. R., ‘On classes of doubly resolvable (v, 3, 2)-BIBDs from balanced tournament designs’, Ars Combin. 24 (1987), 85–91.Google Scholar
[7]Lamken, E. R. and Vanstone, S. A., ‘The existence of factored balanced tournament designs’, Ars Combin. 19 (1985), 157–160.Google Scholar
[8]Lamken, E. R. and Vanstone, S. A., ‘Partitioned balanced tournament designs of side 4n + 1’, Ars Combin. 20 (1985), 29–44.Google Scholar
[9]Lamken, E. R. and Vanstone, S. A., ‘The existence of partitioned balanced tournament designs of side 4n + 3’, Ann. Discrete Math. 34 (1987), 319–338.Google Scholar
[10]Lamken, E. R. and Vanstone, S. A., ‘The existence of partitioned balanced tournament designs’, Ann. Discrete Math. 34 (1987), 339–352.Google Scholar
[11]Lamken, E. R. and Vanstone, S. A., ‘Balanced tournament designs and resolvable (ν, 3, 2)- BIBD s’, Discrete Math. (to appear).Google Scholar
[12]Lamken, E. R. and Vanstone, S. A., ‘Complementary Howell designs of side 2n and order 2n + 2’, Congr. Numer. 41 (1984), 85–113.Google Scholar
[13]Lamken, E. R. and Vanstone, S. A., ‘Skew transversals in frames’, J. Combin. Math. Combin. Comp. 2 (1987), 37–50.Google Scholar
[14]Mullin, R. C. and Stinson, D. R., ‘Holey SOLSSOMs’, Utilitas Math. 25 (1984), 159–169.Google Scholar
[15]Rosa, A. and Stinson, D. R., ‘One-factorizations of regular graphs and Howell designs of small order’, Utilitas Math. 29 (1986), 99–124.Google Scholar
[16]Schellenberg, R. J., van Rees, G. H. J., and Vanstone, S. A., ‘The existence of balanced tournament designs’, Ars Combin. 3 (1977), 303–318.Google Scholar
[17]Stinson, D. R., Some classes of frames and the spectrum of skew room squares and Howell designs, (Ph.D. Thesis, University of Waterloo, 1981).Google Scholar
[18]Stinson, D. R., ‘On the existence of skew Room frames of type 2n’, Ars Combin. 24 (1987), 115–128.Google Scholar
[19]Stinson, D. R. and Zhu, L., ‘On sets of three MOLs with holes’, Discrete Math. 54 (1985), 321–328.CrossRefGoogle Scholar
[20]Stinson, D. R. and Zhu, L., ‘On the existence of MOLs with equal-sized holes’, Aequationes Math. 33 (1987), 96–105.CrossRefGoogle Scholar
[21]Vanstone, S. A., ‘Doubly resolvable designs’, Discrete Math 29 (1980), 77–86.CrossRefGoogle Scholar
[22]Wilson, R. M., ‘Constructions and uses of pairwise balanced designs’, Math. Centre Tracts 55 (1974), 18–41.Google Scholar