A balanced directed cycle design with parameters (υ, k, 1), sometimes called a (υ, k, 1)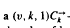-design, is a decomposition of the complete directed graph 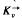into edge disjoint directed cycles of length k. A complete classification is given of (υ, k, 1)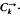-designs admitting the holomorph {øa, b: x ↦ ax + b∣ a, b ∈ Zυ, (a, υ1) = 1} of the cyclic group Zυ as a group of automorphisms. In particular it is shown that such a design exists if and ony if one of (a) k = 2, (b) p ≡ 1 (mod k) for each prime p dividing υ, or (c) k is the least prime dividing υ, k2 does not divide υ, and p ≡ 1 (mod k) for each prime p < k dividing υ.