Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T14:10:58.574Z Has data issue: false hasContentIssue false
  • English
  • Français

Averaging operators on the ring of continuous functions on a compact space1

Published online by Cambridge University Press:  09 April 2009

Barron Brainerd
Barron Brainerd
Affiliation:
Department of Mathematics University of Toronto, Toronto, Canada.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we answer the following question: Given C(X) the latticeordered ring of real continuous functions on the compact Hausdorff space X and T an averaging operator on C(X), under what circumstances can X be decomposed into a topological product 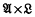such that 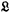supports a measure m and Tf = h where 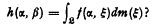By an averaging operator we mean a linear transformation T on C(X) such that: 1. T is positive, that is, if f>0 (f(x) ≧ 0 for all x ∈ and f(x) > 0 for some a ∈ X), then Tf>0. 2. T(fTg) = (Tf)(Tg). 3. T l = 1 where l(x) = 1 for all x ∈ X.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 4 , Issue 3 , August 1964 , pp. 293 - 298
Copyright
Copyright © Australian Mathematical Society 1964

References

[1]Birkhoff, G., Averaging Operators, Symposium in Lattice Theory. Amer. Math. Soc. 1960.Google Scholar
[2]Brainerd, B., On the structure of averaging operators, J. Math. Analysis and Applications, 5 (1962), 347–377.CrossRefGoogle Scholar
[3]MacDowell, R., Banach spaces and algebras of continuous functions, Proc. Amer. Math. Soc. 6 (1955), 67–78.CrossRefGoogle Scholar