Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T23:01:36.211Z Has data issue: false hasContentIssue false
  • English
  • Français

Automatic continuity and second order cohomology

Part of: Topological algebras, normed rings and algebras, Banach algebras Methods of category theory in functional analysis

Published online by Cambridge University Press:  09 April 2009

Volker Runde
Volker Runde
Affiliation:
Department of Mathematical Sciences University of Alberta Edmonton, Alberta T6G 2G1 Canada e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Many Banach algebras A have the property that, although there are discontinuous homomorphisms from A into other Banach algebras, every homomorphism from A into another Banach algebra is automatically continuous on a dense subspace—preferably, a subalgebra—of A. Examples of such algebras are C*-algebras and the group algebras L1(G), where G is a locally compact, abelian group. In this paper, we prove analogous results for 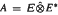, where E is a Banach space, and 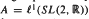. An important rôle is played by the second Hochschild cohomology group of 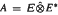and 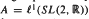, respectively, with coefficients in the one-dimensional annihilator module. It vanishes in the first case and has linear dimension one in the second one.

MSC classification

Secondary: 46H40: Automatic continuity 46M20: Methods of algebraic topology (cohomology, sheaf and bundle theory, etc.)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 68 , Issue 2 , April 2000 , pp. 231 - 243
Copyright
Copyright © Australian Mathematical Society 2000

References

[BC]Bade, W. G. and Curtis, P. C. Jr, ‘Homomorphisms of commutative Banach algebras’, Amer. J. Math. 82 (1960), 589–608.CrossRefGoogle Scholar
[Dal]Dales, H. G., ‘Questions on automatic continuity’, in: Banach algebras '97 (eds. Albrecht, E. and Mathieu, M.) (de Grutyer, 1998) pp. 509–526.CrossRefGoogle Scholar
[DJ]Dales, H. G. and Jarchow, H., ‘Continuity of homomorphisms and derivations from algebras of approximable and nuclear operators’, Math. Proc. Cambridge Phil. Soc. 116 (1994), 465–473.CrossRefGoogle Scholar
[DLW]Dales, H. G., Loy, R. J. and Willis, G. A., ‘Homomorphisms and derivations from B(E)’, J. Funct. Anal. 120 (1994), 201–219.CrossRefGoogle Scholar
[DW]Dales, H. G. and Woodin, W. H., An introduction to independence for analysts (Cambridge University Press, Cambridge, 1987).CrossRefGoogle Scholar
[Dix]Dixon, P. G., ‘Nonseparable Banach algebras whose squares are pathological’, J. Funct. Anal. 26 (1977), 190–200.CrossRefGoogle Scholar
[Gri]Grigorchuk, R. I., ‘Some results on bounded cohomology’, in: Combinatorial and geometric group theory (ed. Duncan, A. J. et al. ) (Cambridge University Press, Cambridge, 1993) pp. 111–163.Google Scholar
[Grø]Grønbæk, N., ‘Morita equivalence for self-induced Banach algebras’, Houston J. Math. 22 (1996), 109–140.Google Scholar
[Gro]Grosser, M., Bidualräume und Vervollständigungen von Banachmoduln (Springer, Berlin, 1979).CrossRefGoogle Scholar
[Hel]Helemskii, A. Ya., The homology of Banach and topological algebras (Kluwer Acad. Publ., Dordrecht, 1989).CrossRefGoogle Scholar
[HR1]Hewitt, E. and Ross, K. A., Abstract harmonic analysis, I (Springer, New York, 1963).Google Scholar
[HR2]Hewitt, E. and Ross, K. A., Abstract harmonic analysis, II (Springer, New York, 1970).Google Scholar
[Joh1]Johnson, B. E., ‘Continuity of homomorphisms of algebras of operators’, J. London Math. Soc. 42 (1967), 537–541.CrossRefGoogle Scholar
[Joh2]Johnson, B. E., ‘Cohomology in Banach algebras’, Mem. Amer. Math. Soc. 127 (Amer. Math. Soc., Providence, 1972).Google Scholar
[Lan]Lang, S., SL2 (R) (Addison-Wesley, 1975).Google Scholar
[MM]Matsumoto, S. and Morita, S., ‘Bounded cohomology of certain groups of homeomorphisms’, Proc. Amer. Math. Soc. 94 (1985), 539–544.CrossRefGoogle Scholar
[Ogd]Ogden, C. P., ‘Homomorphisms from B(Gwn)’, J. London Math. Soc. 54 (1996), 346–358.CrossRefGoogle Scholar
[Rei]Reiter, H., ‘Sur certains idéaux dans L 1(G)’, C. R. Acad. Sci. Paris Sér. A-B 267 (1968), A882–A885.Google Scholar
[Rud]Rudin, W., Functional analysis (McGraw-Hill, New York, 1973).Google Scholar
[Run1]Runde, V., ‘Homomorphisms from L 1 (G) for G ∈ [FIA]− ∪ [Moore]’, J. Funct. Anal. 122 (1994), 25–51.CrossRefGoogle Scholar
[Run2]Runde, V., ‘Interwining operators over L 1 (G) for G ∈ [PG] ∩ [SIN]’, Math. Z. 221 (1996), 495–506.Google Scholar
[Run3]Runde, V., ‘Interwining maps from certain group algebra’, J. London Math. Soc. 57 (1998), 433–448.CrossRefGoogle Scholar
[Sin]Sinclair, A. M., ‘Homomorphisms from C*-algebras’, Proc. London Math. Soc. (3) 32 (1976), 322.CrossRefGoogle Scholar
[Wil1]Willis, G. A., ‘Approximate units in finite codimensionional ideals of group algebras’, J. London Math. Soc. (2) 26 (1982), 143–154.CrossRefGoogle Scholar
[Wil2]Willis, G. A., ‘The continuity of derivations from group algebras: Factorizable and connected groups’, J. Austral. Math. Soc. (Series A) 40 (1992), 185–204.CrossRefGoogle Scholar
[Wil3]Willis, G. A., ‘Compressible operators and the continuity of homomorphisms from algebras of operators’, Studia Math. 115 (1995), 251–259.CrossRefGoogle Scholar