Published online by Cambridge University Press: 09 April 2009
The asymptotic behaviour, for large real positive values of the independent variable t, of solutions of the ordinary differential equation 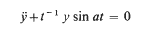 is considered. (The dots denote differentiation with respect to t.) It is shown that this asymptotic behaviour can be obtained by comparison with the differential equation
is considered. (The dots denote differentiation with respect to t.) It is shown that this asymptotic behaviour can be obtained by comparison with the differential equation 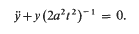 For both equations when a2 < 2 the solutions are unbounded oscillatory functions but when a2 > 2 the solutions are essentially monotone. The critical case a2 = 2 has not been investigated here although the present results suggest that the solutions are probably monotone. The asymptotic estimates of the solutions of equation (1) are first obtained by heuristic means commonly used by Applied Mathematicians working on singular perturbation problems. A basis for a formal expansion is obtained in terms of a recurrence relation and the first few terms are displayed explicitly. These formal expansion estimates are used to guide a rigorous analysis which is essentially an extension of the techniques used in validating solutions obtained by the Langer related equation technique. For the oscillatory case, a pair of Volterra integral equations is used to justify the asymptotic representations for an arbitrary large interval for t but not including the point at infinity.
For both equations when a2 < 2 the solutions are unbounded oscillatory functions but when a2 > 2 the solutions are essentially monotone. The critical case a2 = 2 has not been investigated here although the present results suggest that the solutions are probably monotone. The asymptotic estimates of the solutions of equation (1) are first obtained by heuristic means commonly used by Applied Mathematicians working on singular perturbation problems. A basis for a formal expansion is obtained in terms of a recurrence relation and the first few terms are displayed explicitly. These formal expansion estimates are used to guide a rigorous analysis which is essentially an extension of the techniques used in validating solutions obtained by the Langer related equation technique. For the oscillatory case, a pair of Volterra integral equations is used to justify the asymptotic representations for an arbitrary large interval for t but not including the point at infinity.