Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ibragimov, I. A.
1967.
On Maximum Likelihood Estimation of Parameters of the Spectral Density of Stationary Time Series.
Theory of Probability & Its Applications,
Vol. 12,
Issue. 1,
p.
115.
1970.
Multiple Time Series.
p.
519.
Kashyap, R.
1970.
Maximum likelihood identification of stochastic linear systems.
IEEE Transactions on Automatic Control,
Vol. 15,
Issue. 1,
p.
25.
Dzaparidze, K. O.
1970.
On the Estimation of the Spectral Parameters of a Gaussian Stationary Process with Rational Spectral Density.
Theory of Probability & Its Applications,
Vol. 15,
Issue. 3,
p.
531.
Cleveland, William S.
1972.
The Inverse Autocorrelations of a Time Series and Their Applications.
Technometrics,
Vol. 14,
Issue. 2,
p.
277.
Walker, A. M.
1973.
On the estimation of a harmonic component in a time series with stationary dependent residuals.
Advances in Applied Probability,
Vol. 5,
Issue. 2,
p.
217.
Walker, A. M.
1973.
On the estimation of a harmonic component in a time series with stationary dependent residuals.
Advances in Applied Probability,
Vol. 5,
Issue. 2,
p.
217.
Davies, Robert B.
1973.
Asymptotic inference in stationary Gaussian time-series.
Advances in Applied Probability,
Vol. 5,
Issue. 3,
p.
469.
Hannan, E. J.
1973.
The asymptotic theory of linear time-series models.
Journal of Applied Probability,
Vol. 10,
Issue. 1,
p.
130.
Hannan, E. J.
1973.
The asymptotic theory of linear time-series models.
Journal of Applied Probability,
Vol. 10,
Issue. 1,
p.
130.
Davies, Robert B.
1973.
Asymptotic inference in stationary Gaussian time-series.
Advances in Applied Probability,
Vol. 5,
Issue. 3,
p.
469.
Anderssen, R. S.
and
Bloomfield, Peter
1974.
A Time Series Approach To Numerical Differentiation.
Technometrics,
Vol. 16,
Issue. 1,
p.
69.
Hannan, E.
1974.
Time series analysis.
IEEE Transactions on Automatic Control,
Vol. 19,
Issue. 6,
p.
706.
Hatanaka, Michio
1974.
An efficient two-step estimator for the dynamic adjustment model with autoregressive errors.
Journal of Econometrics,
Vol. 2,
Issue. 3,
p.
199.
Brillinger, D.R.
1974.
Fourier analysis of stationary processes.
Proceedings of the IEEE,
Vol. 62,
Issue. 12,
p.
1628.
Dzaparidze, K. O.
1974.
A New Method for Estimating Spectral Parameters of a Stationary Regular Time Series.
Theory of Probability & Its Applications,
Vol. 19,
Issue. 1,
p.
122.
Dzhaparidze, K. O.
1975.
On Simplified Estimators of Unknown Parameters with Good Asymptotic Properties.
Theory of Probability & Its Applications,
Vol. 19,
Issue. 2,
p.
347.
Dunsmuir, W.
and
Hannan, E. J.
1976.
Vector linear time series models.
Advances in Applied Probability,
Vol. 8,
Issue. 2,
p.
339.
Dunsmuir, W.
and
Hannan, E. J.
1976.
Vector linear time series models.
Advances in Applied Probability,
Vol. 8,
Issue. 2,
p.
339.
Dent, Warren
and
Min, An-Sik
1978.
A Monte Carlo study of autoregressive integrated moving average processes.
Journal of Econometrics,
Vol. 7,
Issue. 1,
p.
23.


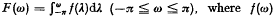 is the spectral density function. It is well known that {x
is the spectral density function. It is well known that {x