Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T21:16:42.109Z Has data issue: false hasContentIssue false
  • English
  • Français

The arithmetic of a semigroup of series of Walsh functions

Part of: Probability theory on algebraic and topological structures Nontrigonometric harmonic analysis Abstract harmonic analysis

Published online by Cambridge University Press:  09 April 2009

I. P. Il'inskaya
I. P. Il'inskaya
Affiliation:
Kharkov State University Department of Mathematics 4 Svobody Square 310077 KharkovUkraine e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 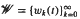be the classical system of the Walsh functions, the multiplicative semigroup of the functions represented by series of functions Wk(t)with non-negative coefficients which sum equals 1. We study the arithmetic of . The analogues of the well-known [ related to the arithmetic of the convolution semigroup of probability measures on the real line are valid in . The classes of idempotent elements, of infinitely divisible elements, of elements without indecomposable factors, and of elements without indecomposable and non-degenerate idempotent factors are completely described. We study also the class of indecomposable elements. Our method is based on the following fact: is isomorphic to the semigroup of probability measures on the groups of characters of the Cantor-Walsh group.

Keywords

probability measures on groupsKhinchin factorization theoremsinfinite divisibilityindecomposabilityWalsh functions

MSC classification

Secondary: 60B15: Probability measures on groups or semigroups, Fourier transforms, factorization 43A25: Fourier and Fourier-Stieltjes transforms on locally compact and other abelian groups 42C10: Fourier series in special orthogonal functions (Legendre polynomials, Walsh functions, etc.)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 68 , Issue 3 , June 2000 , pp. 365 - 378
Copyright
Copyright © Australian Mathematical Society 2000

References

[1]Edwards, R. E., Fourier series. A modern introduction, vol. 2 (Springer, New York, 1982).CrossRefGoogle Scholar
[2]Fel'dman, G. M., Arithmetic of probability distributions and characterization problems on Abelian groups, Transl. Math. Monographs 116 (Amer. Math. Soc., Providence, R.I., 1993).CrossRefGoogle Scholar
[3]Hewitt, E. and Ross, K. A., Abstract harmonic analysis, vol. 1 (Springer, Berlin, 1963).Google Scholar
[4]Il'inskaya (Trukhina), I. P., ‘Arithmetic of a semigroups of series in Legendre functions of the second kind’, Turkish J. Math. 21 (1997), 357–373.Google Scholar
[5]Kaczmarz, S. and Steinhaus, H., Theorie der Orthogonalreien (Z subwencji funduszu kultury narodowej, Warszawa, 1935).Google Scholar
[6]Kashin, B. S. and Saakyan, A. A., Orthogonal series (Nauka, Moscow, 1984) (in Russian).Google Scholar
[7]Kendall, D. G., ‘Delphic semigroups, infinitely divisible regenerative phenomena, and the arithmetic of p-functions’, Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 9 (1967), 163–195.Google Scholar
[8]Kendall, D. G., A tribute to the memory of Rolla Davidson (Willey and Sons, London, 1975).Google Scholar
[9]Linnik, Ju. V. and Ostrovskii, I. V., Decomposition of random variables and vectors, Transl. Math. Monographs 48 (Amer. Math. Soc., Providence, R.I., 1977).Google Scholar
[10]Ostrovskii, I. V., ‘The arithmetic of probability distributions’, Theory Probab. Appl. 31 (1986), 1–24.Google Scholar
[11]Parthasarathy, K. R., Rao, R. R. and Varadhan, S. R. S., ‘On the category of indecomposable distributions on topological groups’, Trans. Amer. Math. Soc. 102 (1962), 200–217.CrossRefGoogle Scholar
[12]Parthasarathy, K. R., Rao, R. R. and Varadhan, S. R. S., ‘Probability distributions on locally compact abelian groups’, Illinois J. Math. 7 (1963), 337–369.CrossRefGoogle Scholar
[13]Thrukhina, I. P., ‘On a problem connected with the arithmetic of probability measures on spheres’, Zap. Nauch. Sem. Leningrad. Otdel. Mat. Inst. Steklov (LOMI) 87 (1979), 143–158 (in Russian).Google Scholar
[14]Thrukhina, I. P., ‘Arithmetic of spherically symmetric measures in the Lobachevskii space’, Teor. Funktsii Funktsional. Anal. i Prilozhen. 34 (1980), 136–146 (in Russian).Google Scholar
[15]Urbanik, K., ‘Generalized convolutions’, Studia Math. 23 (1963), 217–245.Google Scholar