The 3-metabelian groups are those groups in which every subgroup generated by three elements is metabelian. In [2] it was stated and it [3] it was proved that the variety of such groups may be defined by the one law (by [a, b, c, d] we mean [[a, b], [c, d]], and for other definitions and notation we refer to [1]). Recently Bachmuth and Lewin obtained in [1] the surprising and remarkable result that the same variety is defined by the law 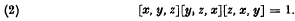Now (2) is reminiscent of the relation 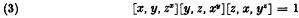which holds in all groups and which is apparently due to Philip Hall. Using the identities 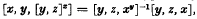, etc., we find that (2) is equivalent to 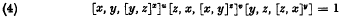where u = [z, x, y] and v = [y, z, z] [z, x, y]. Note that apart from certain displeasing conjugates (4) is curiously similar to both (1) and (2).