Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-23T02:54:59.223Z Has data issue: false hasContentIssue false
  • English
  • Français

Another characteristic conjugacy class of subgroups of finite soluble groups

Published online by Cambridge University Press:  09 April 2009

A. Makan
A. Makan
Affiliation:
Department of MathematicsInstitute of Advanced StudiesAustralian National UniversityP.O. Box 4, CANBERRA
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 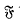name be a class of finite soluble groups with the properties: (1) 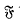is a Fitting class (i.e. normal subgroup closed and normal product closed) and (2) if N ≦ H ≦ G ∈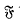, N ⊲ G and H/N is a p-group for some prime p, then H ∈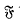. Then 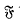is called a Fischer class. In any finite soluble group G, there exists a unique conjugacy class of maximal 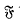-subgroups V called the 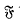-injectors which have the property that for every N◃◃G, N ∩ V is a maximal 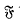-subgroup of N [3]. 3. By Lemma 1 (4) [7] an 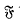-injector V of G covers or avoids a chief factor of G. As in [7] we will call a chief factor 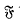-covered or 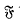-avoided according as V covers or avoids it and 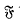-complemented if it is complemented and each of its complements contains some 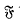-injector. Furthermore we will call a chief factor partially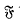-complemented if it is complemented and at least one of its complements contains some 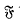-injector of G.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 11 , Issue 4 , November 1970 , pp. 395 - 400
Copyright
Copyright © Australian Mathematical Society 1970

References

[1]Carter, R. W. and Hawkes, T. O., ‘The -normalizers of a finite soluble group’, J. Algebra 5 (1967), 175–202.CrossRefGoogle Scholar
[2]Carter, R. W., Fischer, B. and Hawkes, T. O., ‘Extreme classes of finite soluble groups’, J. Algebra 9 (1968), 285–313.CrossRefGoogle Scholar
[3]Fischer, B., Gaschütz, W. and Hartley, B., ‘Injektoren endlicher auflösbarer Gruppen’, Math. Z. 102 (1967), 337–339.CrossRefGoogle Scholar
[4]Gaschütz, W., ‘Praefrattinigruppen’, Arch. Math. 13 (1962), 418–426.CrossRefGoogle Scholar
[5]Gaschütz, W., ‘Zur Theorie der endlicher auflösbarer Gruppen’, Math. Z. 80 (1963), 300–305.CrossRefGoogle Scholar
[6]Hall, P., ‘On the Sylow system of a soluble group’, Proc. London Math. Soc. (2) 43 (1937), 316–323.Google Scholar
[7]Hartley, B., ‘On Fischer's dualization of Formation Theory’, Proc. London Math. Soc. (3) 19 (1969), 193–207.CrossRefGoogle Scholar
[8]Hawkes, T. O., ‘Analogues of Prefrattini subgroups’, Proc. Internat. Conf. Theory of Groups, Austral. Nat. Univ. Canberra, 08 1965, pp. 145–150.Google Scholar
[9]Mann, A., ‘A Criterion for Pronormality’, J. London Math. Soc. 44 (1969), 175–176.CrossRefGoogle Scholar