Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-20T06:37:09.435Z Has data issue: false hasContentIssue false
  • English
  • Français

An unbounded spectral mapping theorem

Published online by Cambridge University Press:  09 April 2009

S. J. Bernau
S. J. Bernau
Affiliation:
University of OtagoDunedin, New Zealand
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recall that the spectrum, σ(T), of a linear operator T in a complex Banach space is the set of complex numbers λ such that T—λI does not have a densely defined bounded inverse. It is known [7, § 5.1] that σ(T) is a closed subset of the complex plane C. If T is not bounded, σ(T) may be empty or the whole of C. If σ(T) ≠ C and T is closed the spectral mapping theorem, 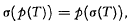is valid for complex polynomials p(z) [7, §5.7]. Also, if T is closed and λ ∉ σ(T), (T–λI)−1 is everywhere defined.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 8 , Issue 1 , February 1968 , pp. 119 - 127
Copyright
Copyright © Australian Mathematical Society 1968

References

[1]Bernau, S. J., ‘The spectral theorem for normal operators’, J. London Math. Soc. 40 (1965), 478–486.CrossRefGoogle Scholar
[2]Bernau, S. J., ‘The square root of a positive self-adjoint operator’, J. Austral. Math. Soc. 8 (1967), 17–36.CrossRefGoogle Scholar
[3]Bernau, S. J., ‘The spectral theorem for unbounded normal operators’, Pacific J. Math. 19 (1966), 391–406.CrossRefGoogle Scholar
[4]Dunford, N. and Schwartz, J. T., Linear Operators, Part I (Interscience, New York, 1958).Google Scholar
[5]Dunford, N. and Schwartz, J. T., Linear Operators, Part II (Interscience, New York, 1963).Google Scholar
[6]Halmos, P. R., Introduction to Hilbert space and the theory of spectral multiplicity (2nd. edition, Chelsea, New York, 1951)Google Scholar
[7]Taylor, A. E., Introduction to functional analysis (Wiley, New York, 1958).Google Scholar