Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T07:28:20.258Z Has data issue: false hasContentIssue false
  • English
  • Français

An improved bound for BFCp-groups

Published online by Cambridge University Press:  09 April 2009

Peter M. Neumann
Peter M. Neumann
Affiliation:
The Queen's CollegeOxford.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The theme of this paper is a conjecture whose origins go back to work of B. H. Neumann ([5], Theorem 3·1) and his former students I. Wiegold and I. D. Macdonald ([7], [4]). B. H. Neumann proved that if there is a bound to the sizes of conjugacy classes in the group G. that is. if G is a BFC group. then the derived group G′ is finite; Wiegold. and later Macdonald. produced explicit upper bounds for G′ in terms of the maximum n of the sizes of the conjugacy classes in G. The coniecture is that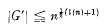 where l(n) should be the arithmetic function1 λ(n) for a best possible bound, or l(n) may be interpreted as log2n for a smooth, monotonicorderof-magnitude estimate. However, the bounds produced in [7] and [4], and even the vastly better upper bounds proved bv Sheooerd and Wieeold [6] for soluble groups, are very much bigger than 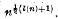, and it is mv aim in this paper to take a first step towards closing the gap. This first, step is study of BFC p-groups: in a sequel I hope to show how the results proved here can be used to obtain improved bounds for arbitrary BFC groups.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 11 , Issue 1 , February 1970 , pp. 19 - 27
Copyright
Copyright © Australian Mathematical Society 1970

References

[1]Bride, I. M., Ph. D. Thesis, University of Manchester Institute of Science and Technology, 1968.Google Scholar
See also: ‘Second mlpotent BFC groups’, J. Australian Math. Soc. 11 (1970), 9–18.CrossRefGoogle Scholar
[2]Michel, Lazard, ‘Sur les groupes mipotents et les anneaux de Lie’, Ann. Sci. Ecoie Norm. Sup. (3) 71 (1954), 101–190.Google Scholar
[3]Livšic, A. H., Calenko, M. S., Šul'geifer, E. G., ‘Varieties in categories’, Mat. Sb. 63 (105) (1964), 554–581 = Amer. Math. Soc. Translations (Series 2) 58, 29–56.Google Scholar
[4]Macdonald, I. D., ‘Some explicit bounds in groups with finite derived groups’, Proc. London Math. Soc. (3) 11 (1961), 23–56.CrossRefGoogle Scholar
[5]Neumann, B. H., ‘Groups covered by permutable subsets’, J. London Math. Soc. 29 (1954), 236–248.CrossRefGoogle Scholar
[6]Shepperd, J. A. H. and Wiegold, James, ‘Transitive permutation groups and groups with finite derived groups’, Math. Zeitschrift 81 (1963), 279–285.CrossRefGoogle Scholar
[7]Wiegold, J., ‘Groups with poundedly finite classes of conjugate elements’, Proc. Roy. Soc. (A) 238 (1957), 389–401.Google Scholar