Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wyman, M.
1972.
Leo Moser 1921-1970.
Canadian Mathematical Bulletin,
Vol. 15,
Issue. 1,
p.
1.
Pach, János
1981.
Graphs whose every independent set has a common neighbour.
Discrete Mathematics,
Vol. 37,
Issue. 2-3,
p.
217.
Frankl, Peter
and
Pach, János
1984.
On disjointly representable sets.
Combinatorica,
Vol. 4,
Issue. 1,
p.
39.
Ananchuen, W.
and
Caccetta, L.
1995.
A note on graphs with a prescribed adjacency property.
Bulletin of the Australian Mathematical Society,
Vol. 51,
Issue. 1,
p.
5.
1995.
Combinatorial Geometry.
p.
319.
Mendel, Manor
and
Naor, Assaf
2006.
Ramsey partitions and proximity data structures.
p.
109.
Baswana, Surender
and
Kavitha, Telikepalli
2006.
Faster Algorithms for Approximate Distance Oracles and All-Pairs Small Stretch Paths.
p.
591.
Bollobás, Béla
and
Scott, Alex
2017.
On a problem of Erdős and Moser.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 87,
Issue. 2,
p.
213.
Malek, Md Faizul Khalid Abd
Anwar, Rusmadiah
and
Hashim, Hema Zulaika
2024.
Achieving Sustainable Business Through AI, Technology Education and Computer Science.
Vol. 163,
Issue. ,
p.
245.
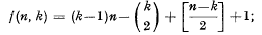 then f0(n, k) = f(n, k).
then f0(n, k) = f(n, k).