Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-29T12:19:22.831Z Has data issue: false hasContentIssue false
  • English
  • Français

AN EXAMPLE OF THE JANTZEN FILTRATION OF A D-MODULE

Part of: Lie algebras and Lie superalgebras (Co)homology theory Lie groups

Published online by Cambridge University Press:  11 November 2024

SIMON BOHUN  and
ANNA ROMANOV Open the ORCID record for ANNA ROMANOV [Opens in a new window]
SIMON BOHUN
Affiliation:
University of Utah, 201 Presidents’ Cir, Salt Lake City, UT 84112, USA e-mail: [email protected]
ANNA ROMANOV*
Affiliation:
The University of New South Wales, Sydney NSW 2033, Australia
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We compute the Jantzen filtration of a 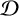$\mathcal {D}$-module on the flag variety of 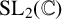$\operatorname {\mathrm {SL}}_2(\mathbb {C})$. At each step in the computation, we illustrate the 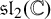$\mathfrak {sl}_2(\mathbb {C})$-module structure on global sections to give an algebraic picture of this geometric computation. We conclude by showing that the Jantzen filtration on the 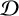$\mathcal {D}$-module agrees with the algebraic Jantzen filtration on its global sections, demonstrating a famous theorem of Beilinson and Bernstein.

Keywords

representations of complex Lie algebrasWhittaker modulesJantzen filtrationBeilinson–Bernstein localisationmonodromic 𝒟-modules

MSC classification

Primary: 14F10: Differentials and other special sheaves; D-modules; Bernstein-Sato ideals and polynomials
Secondary: 17B10: Representations, algebraic theory (weights) 22E47: Representations of Lie and real algebraic groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , First View , pp. 1 - 32
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Communicated by Oded Yacobi

References

Adams, J. D., van Leeuwen, M. A., Trapa, P. E. and Vogan, D. A. Jr, ‘Unitary representations of real reductive groups’, Astérisque 417 (2020), viii + 188.Google Scholar
Barbasch, D., ‘Filtrations on Verma modules’, Ann. Sci. Éc. Norm. Supér. (4) 16 (1983), 489–494.CrossRefGoogle Scholar
Beilinson, A. and Bernstein, J., ‘Localisation de g-modules’, C. R. Math. Acad. Sci. Paris 292 (1981), 15–18.Google Scholar
Beilinson, A. and Bernstein, J., ‘A proof of Jantzen conjectures’, in: Seminar, Advances in Soviet Mathematics, 16 (ed. Gel’fand, I. M.) (American Mathematical Society, Providence, RI, 1993), 1–50.Google Scholar
Beilinson, A. A., ‘How to glue perverse sheaves’, in: K-Theory, Arithmetic and Geometry: Moscow, 1984–1986, Lecture Notes in Mathematics, 1289 (Springer, Berlin–Heidelberg, 1987), 42–51.CrossRefGoogle Scholar
Beilinson, A. and Ginzburg, V., ‘Wall-crossing functors and D–modules’, Represent. Theory Amer. Math. Soc. 3(1) (1999), 1–31.CrossRefGoogle Scholar
Chriss, N. and Ginzburg, V., Representation Theory and Complex Geometry, Modern Birkhäuser Classics (Birkhäuser, Boston, MA, 2010).CrossRefGoogle Scholar
Deligne, P., ‘La conjecture de Weil: II’, Publ. Math. Inst. Hautes Études Sci. 52 (1980), 137–252.CrossRefGoogle Scholar
Gabber, O. and Joseph, A., ‘Towards the Kazhdan–Lusztig conjecture’, Ann. Sci. Éc. Norm. Supér. (4) 14(3) (1981), 261–302.CrossRefGoogle Scholar
Hotta, R., Takeuchi, K. and Tanisaki, T., D-Modules, Perverse Sheaves, and Representation Theory, Progress in Mathematics, 236 (Birkhäuser, Boston, MA, 2008).CrossRefGoogle Scholar
Humphreys, J. E., Representations of Semisimple Lie algebras in the BGG Category, Graduate Studies in Mathematics, 94 (American Mathematical Society, Providence, RI, 2008).CrossRefGoogle Scholar
Iohara, K. and Koga, Y., Representation Theory of the Virasoro Algebra, Springer Monographs in Mathematics (Springer, London, 2011).CrossRefGoogle Scholar
Jantzen, J. C., Moduln mit einem höchsten Gewicht, Lecture Notes in Mathematics, 750 (Springer, Berlin, 1979).CrossRefGoogle Scholar
Kazhdan, D. and Lusztig, G., ‘Representations of Coxeter groups and Hecke algebras’, Invent. Math. 53(2) (1979), 165–184.CrossRefGoogle Scholar
Kübel, J., ‘From Jantzen to Andersen filtration via tilting equivalence’, Math. Scand. 110(2) (2012), 161–180.CrossRefGoogle Scholar
Kübel, J., ‘Tilting modules in category and sheaves on moment graphs’, J. Algebra 371 (2012), 559–576.CrossRefGoogle Scholar
Levasseur, T. and Stafford, J. T., ‘Differential operators and cohomology groups on the basic affine space’, in Studies in Lie Theory, Progress in Mathematics, 243 (Birkhäuser, Boston, MA, 2006), 377–403.CrossRefGoogle Scholar
Miličić, D., Lectures on algebraic theory of D-modules, unpublished manuscript. Available at http://math.utah.edu/milicic.Google Scholar
Miličić, D. and Pandžić, P., ‘Equivariant derived categories, Zuckerman functors and localization’ in: Geometry and Representation Theory of Real and {p}-Adic Groups, Progress in Mathematics, 158 (eds. Tirao, J., Vogan, D. A. and Wolf, J. A.) (Birkhäuser, Boston, MA, 1998), 209–242.CrossRefGoogle Scholar
Romanov, A., ‘Four examples of Beilinson–Bernstein localization’, in: Lie Groups, Number Theory, and Vertex Algebras, Contemporary Mathematics, 768 (American Mathematical Society, Providence, RI, 2021), 65–85.CrossRefGoogle Scholar
Saito, M., ‘Modules de Hodge polarisables’, Publ. Res. Inst. Math. Sci. 24(6) (1988), 849–995.CrossRefGoogle Scholar
Saito, M., ‘Mixed Hodge modules’, Publ. Res. Inst. Math. Sci. 26(2) (1990), 221–333.CrossRefGoogle Scholar
Shapovalov, N. N., ‘On a bilinear form on the universal enveloping algebra of a complex semisimple Lie algebra’, Funct. Anal. Appl. 6(4) (1972), 307–312.CrossRefGoogle Scholar
Soergel, W., ‘Andersen filtration and hard Lefschetz’, Geom. Funct. Anal. 17(6) (2008), 2066–2089.CrossRefGoogle Scholar
Williamson, G., ‘Local Hodge theory of Soergel bimodules’, Acta Math. 217(2) (2016), 341–404.CrossRefGoogle Scholar