Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Blanchard, Paul
1984.
Complex analytic dynamics on the Riemann sphere.
Bulletin of the American Mathematical Society,
Vol. 11,
Issue. 1,
p.
85.
Baker, I. N.
1985.
Some entire functions with multiply-connected wandering domains.
Ergodic Theory and Dynamical Systems,
Vol. 5,
Issue. 2,
p.
163.
Herman, Michael R.
1985.
Are there critical points on the boundaries of singular domains?.
Communications in Mathematical Physics,
Vol. 99,
Issue. 4,
p.
593.
Devaney, Robert L.
and
Tangerman, Folkert
1986.
Dynamics of entire functions near the essential singularity.
Ergodic Theory and Dynamical Systems,
Vol. 6,
Issue. 4,
p.
489.
Kotus, J.
1987.
Dynamical Systems.
Vol. 287,
Issue. ,
p.
10.
Haeseler, F. v.
and
Peitgen, H. O.
1988.
Newton's method and complex dynamical systems.
Acta Applicandae Mathematicae,
Vol. 13,
Issue. 1-2,
p.
3.
Baker, I. N.
1988.
Infinite limits in the iteration of entire functions.
Ergodic Theory and Dynamical Systems,
Vol. 8,
Issue. 4,
p.
503.
v. Haeseler, F.
and
Peitgen, H.-O.
1988.
Newton’s Method and Dynamical Systems.
p.
3.
Blanchard, Paul
and
Chiu, Amy
1991.
Fractal Geometry and Analysis.
p.
45.
Bergweiler, Walter
1993.
Newton's method and a class of meromorphic functions without wandering domains.
Ergodic Theory and Dynamical Systems,
Vol. 13,
Issue. 2,
p.
231.
Hinkkanen, A.
1993.
Julia sets of rational functions are uniformly perfect.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 113,
Issue. 3,
p.
543.
Bergweiler, Walter
1993.
Iteration of meromorphic functions.
Bulletin of the American Mathematical Society,
Vol. 29,
Issue. 2,
p.
151.
Bergweiler, Walter
and
Terglane, Norbert
1996.
Weakly repelling fixpoints and the connectivity of wandering domains.
Transactions of the American Mathematical Society,
Vol. 348,
Issue. 1,
p.
1.
Baker, I.N.
and
Dominguez, P.
1998.
Analytic self-maps of the punctured plane.
Complex Variables, Theory and Application: An International Journal,
Vol. 37,
Issue. 1-4,
p.
67.
Bergweiler, Walter
and
Wang, Yuefei
1998.
On the dynamics of composite entire functions.
Arkiv för Matematik,
Vol. 36,
Issue. 1,
p.
31.
Wang, Yuefei
1999.
Wandering domains in the dynamics of certain meromorphic functions.
Bulletin of the Australian Mathematical Society,
Vol. 59,
Issue. 1,
p.
99.
KAPOOR, G. P.
and
PRASAD, M. GURU PREM
1999.
CHAOTIC BURST IN THE DYNAMICS OF A CLASS OF NONCRITICALLY FINITE ENTIRE FUNCTIONS.
International Journal of Bifurcation and Chaos,
Vol. 09,
Issue. 06,
p.
1137.
Singh, Anand Prakash
2000.
Unbounded components of the fatou set.
Complex Variables, Theory and Application: An International Journal,
Vol. 41,
Issue. 2,
p.
133.
Niamsup, Piyapong
2000.
Julia Sets of Certain Exponential Functions.
Journal of Mathematical Analysis and Applications,
Vol. 250,
Issue. 2,
p.
598.
Wang, Yuefei
2001.
Wandering domains in the transcendental dynamics.
Chinese Science Bulletin,
Vol. 46,
Issue. 1,
p.
34.
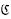 of those points where {fn(z)} forms a normal family is a proper subset of the plane and is invariant under the map z → f(z). A component G of
of those points where {fn(z)} forms a normal family is a proper subset of the plane and is invariant under the map z → f(z). A component G of 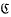 is a wandering domain of f if fn(G)∩fn(G) = Ø for all k ≧ 1, n ≧ 1, k ≠ n. The paper contains the construction of a transcendental entire function which has wandering domains.
is a wandering domain of f if fn(G)∩fn(G) = Ø for all k ≧ 1, n ≧ 1, k ≠ n. The paper contains the construction of a transcendental entire function which has wandering domains.