Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T13:40:07.460Z Has data issue: false hasContentIssue false
  • English
  • Français

AN EIGENSPACE OF LARGE DIMENSION FOR A HECKE ALGEBRA ON AN 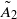BUILDING

Part of: Finite geometry and special incidence structures Abstract harmonic analysis

Published online by Cambridge University Press:  28 September 2011

A. M. MANTERO  and
A. ZAPPA
A. M. MANTERO
Affiliation:
D. S. A., Facoltà di Architettura, Università di Genova, Salita Sant’Agostino 37,16123 Genova, Italy (email: [email protected])
A. ZAPPA*
Affiliation:
D. I. M. A., Università di Genova, Via Dodecaneso 35, 16146 Genova, Italy (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Δ be an affine building of type 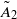and let 𝔸 be its fundamental apartment. We consider the set 𝕌0 of vertices of type 0 of 𝔸 and prove that the Hecke algebra of all W0-invariant difference operators with constant coefficients acting on 𝕌0 has three generators. This property leads us to define three Laplace operators on vertices of type 0 of Δ. We prove that there exists a joint eigenspace of these operators having dimension greater than ∣W0 ∣. This implies that there exist joint eigenfunctions of the Laplacians that cannot be expressed, via the Poisson transform, in terms of a finitely additive measure on the maximal boundary Ω of Δ.

Keywords

buildingsHecke algebrasLaplace operatorsPoisson kernel

MSC classification

Secondary: 51E24: Buildings and the geometry of diagrams 43A80: Analysis on other specific Lie groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 91 , Issue 1 , August 2011 , pp. 29 - 54
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2011

References

[1]Cartwright, D. I. and Młotkowski, W., ‘Harmonic analysis for groups acting on triangle buildings’, J. Aust. Math. Soc. A 56 (1994), 345–383.Google Scholar
[2]Helgason, S., ‘A duality for symmetric spaces with applications to group representations’, Adv. Math. 5 (1970), 1–154.Google Scholar
[3]Kato, S., ‘On eigenspaces of the Hecke algebra with respect to a good maximal compact subgroup of a p-adic reductive group’, Math. Ann. 257 (1981), 1–7.CrossRefGoogle Scholar
[4]Kellil, F. and Rousseau, G., ‘Opérateurs invariants sur certains immeubles affine de rang 2’, Ann. Fac. Sci. Toulouse Math. (6) 16 (2007), 591–610.Google Scholar
[5]Mantero, A. M. and Zappa, A., ‘Spherical functions and spectrum of the Laplace operators on buildings of rank 2’, Boll. Unione Mat. Ital. B (7) 8 (1994), 419–475.Google Scholar
[6]Mantero, A. M. and Zappa, A., ‘Eigenfunctions of the Laplace operators for a building of type ’, J. Geom. Anal. 10 (2000), 339–363.Google Scholar
[7]Mantero, A. M. and Zappa, A., ‘Eigenfunctions of the Laplace operators for a building of type ’, Boll. Unione Mat. Ital. Sez. B Artic. Ric. Mat. (8) 5 (2002), 163–195.Google Scholar
[8]Mantero, A. M. and Zappa, A., ‘Eigenfunctions of the Laplace operators for a building of type ’, Boll. Unione Mat. Ital. (9) 2 (2009), 483–508.Google Scholar
[9]Ronan, M. A., Lectures on Buildings, Perspectives in Mathematics, 7 (Academic Press, London, 1989).Google Scholar