No CrossRef data available.
Published online by Cambridge University Press: 27 March 2014
Let 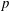 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$ be a prime and
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$ be a prime and 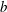 $b$ a primitive root of
$b$ a primitive root of 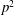 $p^2$. In this paper, we give an explicit formula for the number of times a value in
$p^2$. In this paper, we give an explicit formula for the number of times a value in 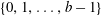 $\{0,1,\ldots,b-1\}$ occurs in the periodic part of the base-
$\{0,1,\ldots,b-1\}$ occurs in the periodic part of the base-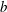 $b$ expansion of
$b$ expansion of 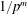 $1/p^m$. As a consequence of this result, we prove two recent conjectures of Aragón Artacho et al. [‘Walking on real numbers’, Math. Intelligencer35(1) (2013), 42–60] concerning the base-
$1/p^m$. As a consequence of this result, we prove two recent conjectures of Aragón Artacho et al. [‘Walking on real numbers’, Math. Intelligencer35(1) (2013), 42–60] concerning the base-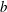 $b$ expansion of Stoneham numbers.
$b$ expansion of Stoneham numbers.