Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T23:02:37.688Z Has data issue: false hasContentIssue false
  • English
  • Français

An approach to nonlinear elliptic boundary value problems

Part of: General theory of linear operators

Published online by Cambridge University Press:  09 April 2009

E. Tarafdar
E. Tarafdar
Affiliation:
Department of Mathematics University of QueenslandSt. Lucia, Queensland, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let D ⊂ Rn be a bounded domain and L: dom L ⊂ L2 (D) → L2 (D) be a self-adjoint operator of finite dimensional kernel. Let f: D × R → R be a function satisfying the Carathéodory condition. Assume that there are constants λ > 0 and δ ∈ [0, 1] such that 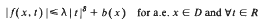and that .

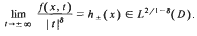Then with the aid of a generalized Krasnosel'skii's theorem it has been proved that under conditions exactly analogous to those of Landesman and Lazer there exists u ∈ L2(D) such that L(u)(x) = f(x, u(x)) for ∀x ∈ D. This result is then used to prove the existence of weak solutions of nonlinesr elliptic boundary value problems.

Other abstract results applicable to ordinary and partial differential equations have also been proved.

MSC classification

Secondary: 47A50: Equations and inequalities involving linear operators, with vector unknowns
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 34 , Issue 3 , June 1983 , pp. 316 - 335
Copyright
Copyright © Australian Mathematical Society 1983

References

[1]Browder, F., Unpublished manuscript mentioned in [14].Google Scholar
[2]de Figueiredo, D. G., Some remarks on the Dirichlet problem elliptic equations (Univ. de Brasilia, Trabalho de Mathematica no. 57 (1974)).Google Scholar
[3]Fučik, S., ‘Nonlinear equations with noninvertible linear part’, Czechoslovak Math. J. 24 (1974), 467–495.CrossRefGoogle Scholar
[4]Fuçik, S., ‘Further remarks on a theorem by E. M. Landesman and A. C. Lazer’, Comment. Math. Univ. Carolinae 15 (1974), 259–271.Google Scholar
[5]Fučik, S., Kučera, M. and Neč, J., ‘Ranges of nonlinear asymptotically linear operators’, J. Differential Equations 17 (1975), 375–394.CrossRefGoogle Scholar
[6]Gaines, R. E. and Mawhin, J. L., Coincidence degree and nonlinear differential equations (Lecture Notes in Mathematics 568, edited by Dold, A. and Eckmann, B., Springer-Verlag (1977)).CrossRefGoogle Scholar
[7]Hess, P., ‘On a theorem by Landesman and Lazer’, Indiana Univ. Math. J. 23 (1974), 827–830.CrossRefGoogle Scholar
[8]Hetzer, G., ‘Some remarks on φ+-operators and on the coincidence degree for a Fredholm equation with noncompact nonlinear pertubations’, Ann. Soc. Sci. Bruxelles Ser. 89 (1975), 497–508.Google Scholar
[9]Hetzer, G., ‘On the existence of weak solutions for some quasilinear elliptic variational boundary value problems at resonance’, Comment. Math. Univ. Carolinae 17 (1976), 315–334.Google Scholar
[10]Landesman, E. M. and Lazer, A. C., ‘Nonlinear perturbations of linear elliptic boundary value problems at resonance’, J. Math. Mech. 19 (1970), 609–623.Google Scholar
[11]Lloyd, N. G., Degree theory (Cambridge University Press, 1978).Google Scholar
[12]Mawhin, J., Equations differentielles et fonctionnelles nonlinéaires, pp. 124–134 (Hermann, Paris 1973).Google Scholar
[13]Nirenberg, L., ‘Generalized degree and nonlinear problems’, Contributions to nonlinear analysis, pp. 1–9, edited by Zarantonello, E. (Academic Press 1971).Google Scholar
[14]Nirenberg, L., ‘An application of generalized degree to a class of nonlinear problems’, Troisieme Colloq. Analyse Functionelle, pp. 57–74 (Liege 1970).Google Scholar
[15]Schechter, M., ‘A nonlinear elliptic boundary value problems’, Ann. Scuola Norm. Sup. Pisa (3) 27 (1973), 707–716.Google Scholar
[16]Williams, S. A., ‘A sharp sufficient condition for solution of nonlinear elliptic boundary value problem’, J. Differential Equations 8 (1970), 580–586.CrossRefGoogle Scholar