Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-05T02:12:03.471Z Has data issue: false hasContentIssue false
  • English
  • Français

AC-GORENSTEIN RINGS AND THEIR STABLE MODULE CATEGORIES

Part of: Applied homological algebra and category theory Homological methods Homological algebra

Published online by Cambridge University Press:  29 October 2018

JAMES GILLESPIE
JAMES GILLESPIE*
Affiliation:
Ramapo College of New Jersey, School of Theoretical and Applied Science, 505 Ramapo Valley Road, Mahwah, NJ 07430, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We introduce what is meant by an AC-Gorenstein ring. It is a generalized notion of Gorenstein ring that is compatible with the Gorenstein AC-injective and Gorenstein AC-projective modules of Bravo–Gillespie–Hovey. It is also compatible with the notion of $n$-coherent rings introduced by Bravo–Perez. So a 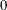$0$-coherent AC-Gorenstein ring is precisely a usual Gorenstein ring in the sense of Iwanaga, while a 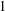$1$-coherent AC-Gorenstein ring is precisely a Ding–Chen ring. We show that any AC-Gorenstein ring admits a stable module category that is compactly generated and is the homotopy category of two Quillen equivalent abelian model category structures. One is projective with cofibrant objects that are Gorenstein AC-projective modules while the other is an injective model structure with fibrant objects that are Gorenstein AC-injectives.

Keywords

Gorenstein ringabelian model categorystable module category

MSC classification

Primary: 16E65: Homological conditions on rings (generalizations of regular, Gorenstein, Cohen-Macaulay rings, etc.)
Secondary: 18G25: Relative homological algebra, projective classes 55U35: Abstract and axiomatic homotopy theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 107 , Issue 2 , October 2019 , pp. 181 - 198
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Bravo, D. and Gillespie, J., ‘Absolutely clean, level, and Gorenstein AC-injective complexes’, Comm. Algebra 44(5) (2016), 2213–2233.Google Scholar
Bravo, D., Gillespie, J. and Hovey, M., ‘The stable module category of a general ring’, Preprint, 2014, arXiv:1405.5768.Google Scholar
Bravo, D. and Pérez, M. A., ‘Finiteness conditions and cotorsion pairs’, J. Pure Appl. Algebra 221(6) (2017), 1249–1267.Google Scholar
Damiano, R. F., ‘Coflat rings and modules’, Pacific J. Math. 81(2) (1979), 349–369.Google Scholar
Ding, N. and Chen, J., ‘The flat dimensions of injective modules’, Manuscripta Math. 78(2) (1993), 165–177.Google Scholar
Ding, N. and Chen, J., ‘Coherent rings with finite self-FP-injective dimension’, Commun. Algebra 24(9) (1996), 2963–2980.Google Scholar
Enochs, E. and Jenda, O., Relative Homological Algebra, De Gruyter Expositions in Mathematics, 30 (Walter De Gruyter, New York, 2000).Google Scholar
Estrada, S. and Gillespie, J., ‘The projective stable category of a coherent scheme’, Proc. Roy. Soc. Edinburgh Sect. A, to appear. Published online (26 February 2018).Google Scholar
Gillespie, J., ‘Model structures on modules over Ding–Chen rings’, Homology, Homotopy Appl. 12(1) (2010), 61–73.Google Scholar
Gillespie, J., ‘Gorenstein complexes and recollements from cotorsion pairs’, Adv. Math. 291 (2016), 859–911.Google Scholar
Gillespie, J., ‘Hereditary abelian model categories’, Bull. Lond. Math. Soc. 48(6) (2016), 895–922.Google Scholar
Gillespie, J., ‘Gorenstain AC-projective chain complexes’, J. Homotopy Relat. Struct., to appear. Published online (20 March 2018).Google Scholar
Gillespie, J. and Hovey, M., ‘Gorenstein model structures and generalized derived categories’, Proc. Edinb. Math. Soc. (2) 53(3) (2010), 675–696.Google Scholar
Glaz, S., Commutative Coherent Rings, Lecture Notes in Mathematics, 1371 (Springer, Berlin, 1989).Google Scholar
Goebel, R. and Trlifaj, J., Approximations and Endomorphism Algebras of Modules, de Gruyter Expositions in Mathematics, 41 (Walter de Gruyter & Co., Berlin, 2006).Google Scholar
Hovey, M., Model Categories, Mathematical Surveys and Monographs, 63 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Hovey, M., ‘Cotorsion pairs, model category structures, and representation theory’, Math. Z. 241 (2002), 553–592.Google Scholar
Iwanaga, Y., ‘On rings with finite self-injective dimension’, Comm. Algebra 7(4) (1979), 393–414.Google Scholar
Iwanaga, Y., ‘On rings with finite self-injective dimension II’, Tsukuba J. Math. 4(1) (1980), 107–113.Google Scholar
Wang, J., Liu, Z. and Yang, X., ‘A negative answer to a Gillespie’s question’, Preprint.Google Scholar
Zhao, T. and Pérez, M. A., ‘Relative FP-injective and FP-flat complexes and their model structures’, Preprint, 2017, arXiv:1703.10703.Google Scholar