Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-25T00:27:50.089Z Has data issue: false hasContentIssue false
  • English
  • Français

ABSTRACT HARMONIC ANALYSIS OF RELATIVE CONVOLUTIONS OVER CANONICAL HOMOGENEOUS SPACES OF SEMIDIRECT PRODUCT GROUPS

Part of: Abstract harmonic analysis

Published online by Cambridge University Press:  16 March 2016

ARASH GHAANI FARASHAHI
ARASH GHAANI FARASHAHI*
Affiliation:
Numerical Harmonic Analysis Group (NuHAG), Faculty of Mathematics, University of Vienna, Vienna, Austria email [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

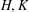This paper presents a structured study for abstract harmonic analysis of relative convolutions over canonical homogeneous spaces of semidirect product groups. Let $H,K$ be locally compact groups and 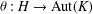$\unicode[STIX]{x1D703}:H\rightarrow \text{Aut}(K)$ be a continuous homomorphism. Let 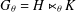$G_{\unicode[STIX]{x1D703}}=H\ltimes _{\unicode[STIX]{x1D703}}K$ be the semidirect product of 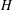$H$ and 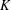$K$ with respect to 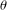$\unicode[STIX]{x1D703}$ and 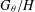$G_{\unicode[STIX]{x1D703}}/H$ be the canonical homogeneous space (left coset space) of 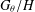$G_{\unicode[STIX]{x1D703}}/H$. We present a unified approach to the harmonic analysis of relative convolutions over the canonical homogeneous space 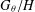$G_{\unicode[STIX]{x1D703}}/H$.

Keywords

canonical homogeneous space of semidirect groupsrho-function𝜃-convolution𝜃-involutionrelative convolutions

MSC classification

Primary: 43A85: Analysis on homogeneous spaces
Secondary: 43A15: $L^p$-spaces and other function spaces on groups, semigroups, etc.
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 101 , Issue 2 , October 2016 , pp. 171 - 187
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Arefijamaal, A. A. and Ghaani Farashahi, A., ‘Zak transform for semidirect product of locally compact groups’, Anal. Math. Phys. 3(3) (2013), 263–276.CrossRefGoogle Scholar
Arefijamaal, A. A. and Kamyabi-Gol, R. A., ‘On construction of coherent states associated with semidirect products’, Int. J. Wavelets Multiresolut. Inf. Process. 6(5) (2008), 749–759.CrossRefGoogle Scholar
Arefijamaal, A. A. and Kamyabi-Gol, R. A., ‘On the square integrability of quasiregular representation on semidirect product groups’, J. Geom. Anal. 19(3) (2009), 541–552.Google Scholar
Chirikjian, G. and Kyatkin, A., Engineering Applications of Noncommutative Harmonic Analysis with Emphasis on Rotation and Motion Groups (CRC Press, Boca Raton, FL, 2001).Google Scholar
Folland, G. B., A Course in Abstract Harmonic Analysis (CRC Press, Boca Raton, FL, 1995).Google Scholar
Ghaani Farashahi, A., ‘Convolution and involution on function spaces of homogeneous spaces’, Bull. Malays. Math. Sci. Soc. (2) 36(4) (2013), 1109–1122.Google Scholar
Ghaani Farashahi, A., ‘Generalized Weyl–Heisenberg (GWH) groups’, Anal. Math. Phys. 4(3) (2014), 187–197.Google Scholar
Ghaani Farashahi, A., ‘A unified group theoretical method for the partial Fourier analysis on semidirect product of locally compact groups’, Results Math. 67(1–2) (2015), 235–251.Google Scholar
Ghaani Farashahi, A., ‘Continuous partial Gabor transform for semidirect product of locally compact groups’, Bull. Malays. Math. Sci. Soc. (2) 38(2) (2015), 779–803.Google Scholar
Ghaani Farashahi, A., ‘Abstract relative function ∗-algebras over canonical homogeneous spaces of semidirect product groups’, Southeast Asian Bull. Math. 40(1) (2016), 1–13.Google Scholar
Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis, Vol. 1 (Springer, Berlin–Heidelberg–New York, 1963).Google Scholar
Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis, Vol. 2 (Springer, Berlin–Heidelberg–New York, 1970).Google Scholar
Hochschild, G., The Structure of Lie Groups (Holden-Day, San Francisco, 1965).Google Scholar
Kisil, V., ‘Connection between two-sided and one-sided convolution type operators on non-commutative groups’, Integral Equations Operator Theory 22(3) (1995), 317–332.Google Scholar
Kisil, V., ‘Relative convolutions. I. Properties and applications’, Adv. Math. 147(1) (1999), 35–73.Google Scholar
Kisil, V., Geometry of Möbius Transformations. Elliptic, Parabolic and Hyperbolic Actions of SL 2(ℝ) (Imperial College Press, London, 2012).CrossRefGoogle Scholar
Kisil, V., ‘The real and complex techniques in harmonic analysis from the point of view of covariant transform’, Eurasian Math. J. 5(1) (2014), 95–121.Google Scholar
Kisil, V., ‘Calculus of operators: covariant transform and relative convolutions’, Banach J. Math. Anal. 8(2) (2014), 156–184.Google Scholar
Reiter, H. and Stegeman, J. D., Classical Harmonic Analysis, 2nd edn (Oxford University Press, New York, 2000).Google Scholar