Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-05T02:59:31.131Z Has data issue: false hasContentIssue false
  • English
  • Français

ZERO JORDAN PRODUCT DETERMINED BANACH ALGEBRAS

Part of: Topological algebras, normed rings and algebras, Banach algebras Abstract harmonic analysis Selfadjoint operator algebras

Published online by Cambridge University Press:  08 January 2020

J. ALAMINOS ,
M. BREŠAR ,
J. EXTREMERA  and
A. R. VILLENA
J. ALAMINOS
Affiliation:
Departamento de Análisis, Matemático, Facultad de Ciencias, Universidad de Granada, 18071Granada, Spain e-mail: [email protected]
M. BREŠAR
Affiliation:
Faculty of Mathematics and Physics, University of Ljubljana, Jadranska 19, 1000Ljubljana, Slovenia Faculty of Natural Sciences and Mathematics, University of Maribor, Koroška 160, 2000Maribor, Slovenia e-mail: [email protected]
J. EXTREMERA
Affiliation:
Departamento de Análisis, Matemático, Facultad de Ciencias, Universidad de Granada, 18071Granada, Spain e-mail: [email protected]
A. R. VILLENA
Affiliation:
Departamento de Análisis, Matemático, Facultad de Ciencias, Universidad de Granada, 18071Granada, Spain e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A Banach algebra 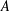$A$ is said to be a zero Jordan product determined Banach algebra if, for every Banach space 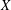$X$, every bilinear map 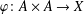$\unicode[STIX]{x1D711}:A\times A\rightarrow X$ satisfying 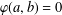$\unicode[STIX]{x1D711}(a,b)=0$ whenever $a$, 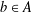$b\in A$ are such that 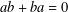$ab+ba=0$, is of the form 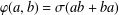$\unicode[STIX]{x1D711}(a,b)=\unicode[STIX]{x1D70E}(ab+ba)$ for some continuous linear map $\unicode[STIX]{x1D70E}$. We show that all 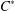$C^{\ast }$-algebras and all group algebras 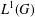$L^{1}(G)$ of amenable locally compact groups have this property and also discuss some applications.

Keywords

C∗ -algebragroup algebrazero Jordan product determined Banach algebrazero product determined Banach algebrasymmetrically amenable Banach algebraweakly amenable Banach algebra

MSC classification

Primary: 43A20: $L^1$-algebras on groups, semigroups, etc.
Secondary: 46H05: General theory of topological algebras 46L05: General theory of $C^*$-algebras
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 111 , Issue 2 , October 2021 , pp. 145 - 158
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by A. Sims

The authors were supported by MINECO grant PGC2018-093794-B-I00. The first, the third and the fourth named authors were supported by Junta de Andalucía grant FQM-185. The second named author was supported by ARRS grant P1-0288.

References

Alaminos, J., Brešar, M., Extremera, J., Špenko, Š. and Villena, A. R., ‘Commutators and square-zero elements in Banach algebras’, Q. J. Math. 67 (2016), 1–13.Google Scholar
Alaminos, J., Brešar, M., Extremera, J. and Villena, A. R., ‘Maps preserving zero products’, Studia Math. 193 (2009), 131–159.Google Scholar
Alaminos, J., Brešar, M., Extremera, J. and Villena, A. R., ‘Zero Lie product determined Banach algebras’, Studia Math. 239 (2017), 189–199.Google Scholar
Alaminos, J., Brešar, M., Extremera, J. and Villena, A. R., ‘Zero Lie product determined Banach algebras, II’, J. Math. Anal. Appl. 474 (2019), 1498–1511.Google Scholar
An, G., Li, J. and He, J., ‘Zero Jordan product determined algebras’, Linear Algebra Appl. 475 (2015), 90–93.Google Scholar
Brešar, M., Introduction to Noncommutative Algebra, Universitext (Springer, Cham, 2014).Google Scholar
Brešar, M., ‘Finite dimensional zero product determined algebras are generated by idempotents’, Expo. Math. 34 (2016), 130–143.Google Scholar
Brešar, M., Grašič, M. and Sanchez, J., ‘Zero product determined matrix algebras’, Linear Algebra Appl. 430 (2009), 1486–1498.Google Scholar
Dales, H. G., Banach Algebras and Automatic Continuity, London Mathematical Society Monographs New Series, 24 (Oxford Science Publications, The Clarendon Press, Oxford University Press, New York, 2000).Google Scholar
Johnson, B. E., ‘Symmetric amenability and the nonexistence of Lie and Jordan derivations’, Math. Proc. Cambridge Philos. Soc. 120 (1996), 455–473.Google Scholar
Read, C. J., ‘Discontinuous derivations on the algebra of bounded operators on a Banach space’, J. Lond. Math. Soc. (2) 40 (1989), 305–326.Google Scholar