Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T15:51:39.578Z Has data issue: false hasContentIssue false
  • English
  • Français

WEIGHTED CORE–EP INVERSE AND WEIGHTED CORE–EP PRE-ORDERS IN A $C^{\ast }$-ALGEBRA

Part of: Topological algebras, normed rings and algebras, Banach algebras Basic linear algebra

Published online by Cambridge University Press:  18 October 2019

DIJANA MOSIĆ
DIJANA MOSIĆ*
Affiliation:
Department of Mathematics, Faculty of Sciences and Mathematics, University of Niš, P.O. Box 224, 18000 Niš, Serbia e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

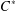We define extensions of the weighted core–EP inverse and weighted core–EP pre-orders of bounded linear operators on Hilbert spaces to elements of a 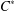$C^{\ast }$-algebra. Some properties of the weighted core–EP inverse and weighted core–EP pre-orders are generalized and some new ones are proved. Using the weighted element, the weighted core–EP pre-order, the minus partial order and the star partial order of certain elements, new weighted pre-orders are presented on the set of all 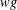$wg$-Drazin invertible elements of a 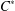$C^{\ast }$-algebra. Applying these results, we introduce and characterize new partial orders which extend the core–EP pre-order to a partial order.

Keywords

weighted core–EP inversewg-Drazin inversecore–EP pre-orderminus partial orderstar partial order

MSC classification

Primary: 46H05: General theory of topological algebras
Secondary: 46H99: None of the above, but in this section 15A09: Matrix inversion, generalized inverses
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 111 , Issue 1 , August 2021 , pp. 76 - 110
Check for updates
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by L. O. Clark

The author is supported by the Ministry of Education, Science and Technological Development, Republic of Serbia, grant no. 174007.

References

Baksalary, O. M. and Trenkler, G., ‘Core inverse of matrices’, Linear Multilinear Algebra 58(6) (2010), 681–697.CrossRefGoogle Scholar
Castro González, N. and Koliha, J. J., ‘New additive results for the g-Drazin inverse’, Proc. Roy. Soc. Edinburgh Sect. A 134 (2004), 1085–1097.CrossRefGoogle Scholar
Dajić, A. and Koliha, J. J., ‘The weighted g-Drazin inverse for operators’, J. Aust. Math. Soc. 82 (2007), 163–181.10.1017/S1446788700016013CrossRefGoogle Scholar
Drazin, M. P., ‘Natural structures on semigroups with involution’, Bull. Amer. Math. Soc. 84 (1978), 139–141.CrossRefGoogle Scholar
Du, H. K. and Deng, C. Y., ‘The representation and characterization of Drazin inverses of operators on a Hilbert space’, Linear Algebra Appl. 407 (2005), 117–124.CrossRefGoogle Scholar
Ferreyra, D. E., Levis, F. E. and Thome, N., ‘Revisiting the core EP inverse and its extension to rectangular matrices’, Quaest. Math. 41(2) (2018), 265–281.10.2989/16073606.2017.1377779CrossRefGoogle Scholar
Gao, Y. and Chen, J., ‘Pseudo core inverses in rings with involution’, Commun. Algebra 46(1) (2018), 38–50.CrossRefGoogle Scholar
Gao, Y., Chen, J. and Ke, Y., ‘∗-DMP elements in ∗-semigroups and ∗-rings’, Filomat 32(9) (2018), 3073–3085.CrossRefGoogle Scholar
Hernández, A., Lattanzi, M. and Thome, N., ‘Weighted binary relations involving the Drazin inverse’, Appl. Math. Comput. 253 (2015), 215–223.Google Scholar
Hernández, A., Lattanzi, M. and Thome, N., ‘On some new pre-orders defined by weighted Drazin inverses’, Appl. Math. Comput. 282 (2016), 108–116.Google Scholar
Koliha, J. J., ‘A generalized Drazin inverse’, Glasgow Math. J. 38 (1996), 367–381.CrossRefGoogle Scholar
Koliha, J. J., ‘Range projections of idempotents in C ∗ -algebras’, Demonstratio Math. 34(1) (2001), 91–103.Google Scholar
Marovt, J., ‘On star, sharp, core, and minus partial orders in Rickart rings’, Banach J. Math. Anal. 10(3) (2016), 495–508.CrossRefGoogle Scholar
Marovt, J., ‘Orders in rings based on the core-nilpotent decomposition’, Linear Multilinear Algebra 66(4) (2018), 803–820.CrossRefGoogle Scholar
Mitsch, H., ‘A natural partial order for semigroups’, Proc. Amer. Math. Soc. 97(3) (1986), 384–388.CrossRefGoogle Scholar
Mosić, D., ‘Core–EP inverse in rings with involution’, Preprint.Google Scholar
Mosić, D., ‘Core–EP pre-order of Hilbert space operators’, Quaest. Math. 41(5) (2018), 585–600.CrossRefGoogle Scholar
Mosić, D., ‘Weighted core–EP inverse of an operator between Hilbert spaces’, Linear Multilinear Algebra 67(2) (2019), 278–298.CrossRefGoogle Scholar
Mosić, D. and Djordjević, D. S., ‘Weighted generalized Drazin inverse in rings’, Georgian Math. J. 23(4) (2016), 587–594.CrossRefGoogle Scholar
Mosić, D. and Djordjević, D. S., ‘The gDMP inverse of Hilbert space operators’, J. Spectr. Theor. 8(2) (2018), 555–573.CrossRefGoogle Scholar
Prasad, K. M. and Mohana, K. S., ‘Core–EP inverse’, Linear Multilinear Algebra 62(6) (2014), 792–802.CrossRefGoogle Scholar
Wang, H. X., ‘Core-EP decomposition and its applications’, Linear Algebra Appl. 508 (2016), 289–300.CrossRefGoogle Scholar
Xu, S. Z., Chen, J. L. and Zhang, X. X., ‘New characterizations for core and dual core inverses in rings with involution’, Front. Math. China 12(1) (2017), 231–246.CrossRefGoogle Scholar