Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-25T15:11:48.388Z Has data issue: false hasContentIssue false
  • English
  • Français

ON POSSIBLE VALUES OF THE INTERIOR ANGLE BETWEEN INTERMEDIATE SUBALGEBRAS

Part of: Selfadjoint operator algebras Linear spaces and algebras of operators

Published online by Cambridge University Press:  17 July 2023

VED PRAKASH GUPTA Open the ORCID record for VED PRAKASH GUPTA [Opens in a new window]  and
DEEPIKA SHARMA
VED PRAKASH GUPTA
Affiliation:
School of Physical Sciences, Jawaharlal Nehru University, New Delhi, India e-mail: [email protected]
DEEPIKA SHARMA*
Affiliation:
School of Physical Sciences, Jawaharlal Nehru University, New Delhi, India
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that all values in the interval 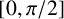$[0,{\pi }/{2}]$ can be attained as interior angles between intermediate subalgebras (as introduced by Bakshi and the first named author [‘Lattice of intermediate subalgebras’, J. Lond. Math. Soc. (2) 104(2) (2021), 2082–2127]) of a certain inclusion of simple unital 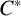$C^*$-algebras. We also calculate the interior angles between intermediate crossed product subalgebras of any inclusion of crossed product algebras corresponding to any action of a countable discrete group and its subgroups on a unital 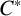$C^*$-algebra.

Keywords

intermediate subalgebrasinterior anglecrossed productsgroup C*-algebrasinclusions of C*-algebrassimple C*-algebrasfinite-index conditional expectationsC*-basic construction

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Secondary: 47L40: Limit algebras, subalgebras of $C^*$-algebras
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 117 , Issue 1 , August 2024 , pp. 44 - 66
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Communicated by Aidan Sims

References

Bakshi, K. C., Das, S., Liu, Z. and Ren, Y., ‘An angle between intermediate subfactors and its rigidity’, Trans. Amer. Math. Soc. 371 (2019), 5973–5991.10.1090/tran/7738CrossRefGoogle Scholar
Bakshi, K. C. and Gupta, V. P., ‘A note on irreducible quadrilaterals of $I{I}_1$ -factors’, Internat. J. Math. 30 (2019), 1950061.10.1142/S0129167X19500617CrossRefGoogle Scholar
Bakshi, K. C. and Gupta, V. P., ‘Lattice of intermediate subalgebras’, J. Lond. Math. Soc. (2) 104(2) (2021), 2082–2127.10.1112/jlms.12492CrossRefGoogle Scholar
Brown, N. P. and Ozawa, N., ${C}^{\ast }$ -Algebras and Finite Dimensional Approximations, Graduate Studies in Mathematics, 88 (American Mathematical Society, Providence, RI, 2008).10.1090/gsm/088CrossRefGoogle Scholar
Choda, M., ‘A correspondence between subgroups and subalgebras in a discrete ${C}^{\ast }$ -crossed product’, Math. Japon. 24(2) (1979/80), 225–229.Google Scholar
Ino, S. and Watatani, Y., ‘Perturbation of intermediate ${C}^{\ast }$ -subalgebras for simple ${C}^{\ast }$ –algebras’, Bull. Lond. Math. Soc. 46 (2014), 469–480.10.1112/blms/bdu001CrossRefGoogle Scholar
Izumi, M., ‘Inclusions of simple ${C}^{\ast }$ -algebras’, J. Reine Angew. Math. 547 (2002), 97–138.Google Scholar
Jones, V. F. R. and Sunder, V. S., Introduction to Subfactors, London Mathematical Society Lecture Note Series, 234 (Cambridge University Press, Cambridge, 1997).10.1017/CBO9780511566219CrossRefGoogle Scholar
Khoshkam, M., ‘Hilbert ${C}^{\ast }$ -modules and conditional expectations on crossed products’, J. Aust. Math. Soc. Ser. A 61 (1996), 106–118.10.1017/S1446788700000100CrossRefGoogle Scholar
Takesaki, M., Theory of Operator Algebras I (Springer-Verlag, New York, 1979).10.1007/978-1-4612-6188-9CrossRefGoogle Scholar
Watatani, Y., Index for ${C}^{\ast }$ -Subalgebras, Memoirs of the American Mathematical Society, 83 (American Mathematical Society, Providence, RI, 1990).Google Scholar
Williams, D. P., Crossed Products of ${C}^{\ast }$ -Algebras, Mathematical Surveys and Monographs, 134 (American Mathematical Society, Providence, RI, 2007).Google Scholar