Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T14:08:48.752Z Has data issue: false hasContentIssue false
  • English
  • Français

ON LINEAR RELATIONS FOR DIRICHLET SERIES FORMED BY RECURSIVE SEQUENCES OF SECOND ORDER

Part of: Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  16 January 2020

CARSTEN ELSNER  and
NICLAS TECHNAU
CARSTEN ELSNER
Affiliation:
University of Applied Sciences, Freundallee 15, D-30173Hanover, Germany e-mail: [email protected]
NICLAS TECHNAU*
Affiliation:
Department of Mathematics, University of York, Heslington, York, YO10 5DD, UK Technische Universität Graz, Institut für Analysis und Zahlentheorie, Steyrergasse 30/II, A-8010Graz, Austria e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 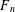$F_{n}$ and 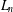$L_{n}$ be the Fibonacci and Lucas numbers, respectively. Four corresponding zeta functions in $s$ are defined by

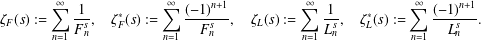$$\begin{eqnarray}\unicode[STIX]{x1D701}_{F}(s):=\mathop{\sum }_{n=1}^{\infty }{\displaystyle \frac{1}{F_{n}^{s}}},\quad \unicode[STIX]{x1D701}_{F}^{\ast }(s):=\mathop{\sum }_{n=1}^{\infty }{\displaystyle \frac{(-1)^{n+1}}{F_{n}^{s}}},\quad \unicode[STIX]{x1D701}_{L}(s):=\mathop{\sum }_{n=1}^{\infty }{\displaystyle \frac{1}{L_{n}^{s}}},\quad \unicode[STIX]{x1D701}_{L}^{\ast }(s):=\mathop{\sum }_{n=1}^{\infty }{\displaystyle \frac{(-1)^{n+1}}{L_{n}^{s}}}.\end{eqnarray}$$
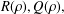As a consequence of Nesterenko’s proof of the algebraic independence of the three Ramanujan functions $R(\unicode[STIX]{x1D70C}),Q(\unicode[STIX]{x1D70C}),$ and 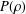$P(\unicode[STIX]{x1D70C})$ for any algebraic number 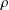$\unicode[STIX]{x1D70C}$ with 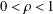$0<\unicode[STIX]{x1D70C}<1$, the algebraic independence or dependence of various sets of these numbers is already known for positive even integers $s$. In this paper, we investigate linear forms in the above zeta functions and determine the dimension of linear spaces spanned by such linear forms. In particular, it is established that for any positive integer $m$ the solutions of
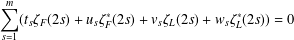$$\begin{eqnarray}\mathop{\sum }_{s=1}^{m}(t_{s}\unicode[STIX]{x1D701}_{F}(2s)+u_{s}\unicode[STIX]{x1D701}_{F}^{\ast }(2s)+v_{s}\unicode[STIX]{x1D701}_{L}(2s)+w_{s}\unicode[STIX]{x1D701}_{L}^{\ast }(2s))=0\end{eqnarray}$$
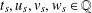 with $t_{s},u_{s},v_{s},w_{s}\in \mathbb{Q}$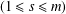$(1\leq s\leq m)$ form a $\mathbb{Q}$-vector space of dimension $m$. This proves a conjecture from the Ph.D. thesis of Stein, who, in 2012, was inspired by the relation 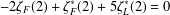$-2\unicode[STIX]{x1D701}_{F}(2)+\unicode[STIX]{x1D701}_{F}^{\ast }(2)+5\unicode[STIX]{x1D701}_{L}^{\ast }(2)=0$. All the results are also true for zeta functions in 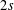$2s$, where the Fibonacci and Lucas numbers are replaced by numbers from sequences satisfying a second-order recurrence formula.

Keywords

Fibonacci and Lucas numberslinear independenceelliptic functionsq-series

MSC classification

Primary: 11J72: Irrationality; linear independence over a field
Secondary: 11J85: Algebraic independence; Gel'fond's method
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 110 , Issue 3 , June 2021 , pp. 406 - 430
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by M. Coons

References

André-Jeannin, R., ‘Irrationalité de la somme des inverses de certaines suites récurrentes’, C. R. Acad. Sci. Paris Sér. I Math. 308 (1989), 539–541.Google Scholar
Borwein, J. M. and Borwein, P. B., Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity, Canadian Mathematical Society Series of Monographs and Advanced Texts, 4 (Wiley, New York, 1987).Google Scholar
Byrd, P. F. and Friedman, M. D., Handbook of Elliptic Integrals for Engineers and Physicists, 2nd edn (Springer, Berlin, 1971).Google Scholar
Duverney, D., Nishioka, Ke., Nishioka, Ku. and Shiokawa, I., ‘Transcendence of Rogers–Ramanujan continued fraction and reciprocal sums of Fibonacci numbers’, Proc. Japan Acad. Ser. A Math. Sci. 73 (1997), 140–142.Google Scholar
Elsner, C., Shimomura, S. and Shiokawa, I., ‘Algebraic relations for reciprocal sums of Fibonacci numbers’, Acta Arith. 130(1) (2007), 37–60.Google Scholar
Elsner, C., Shimomura, S. and Shiokawa, I., ‘Exceptional algebraic relations for reciprocal sums of Fibonacci and Lucas numbers’, in: Diophantine Analysis and Related Fields 2011, AIP Conf. Proc., 1385 (eds. Amou, M. and Katsurada, M.) (AIP, New York, 2011), 17–31.Google Scholar
Elsner, C., Shimomura, S. and Shiokawa, I., ‘Algebraic independence results for reciprocal sums of Fibonacci numbers’, Acta Arith. 148(3) (2011), 205–223.Google Scholar
Nesterenko, Yu. V., ‘Modular functions and transcendence questions’, Mat. Sb. 187 (1996), 65–96; English transl. Sb. Math. 187 (1996), 1319–1348.Google Scholar
Stein, M., ‘Algebraic independence results for reciprocal sums of Fibonacci and Lucas numbers’, PhD Thesis, Gottfried Wilhelm Leibniz Universität Hannover, Fakultät für Mathematik und Physik, 2012. https://www.tib.eu/de/suchen/id/TIBKAT%3A684662426/Algebraic-independence-results-for-reciprocal-sums/.Google Scholar
Zucker, I. J., ‘The summation of series of hyperbolic functions’, SIAM J. Math. Anal. 10 (1979), 192–206.Google Scholar