 $\boldsymbol {L}$-FUNCTIONS
$\boldsymbol {L}$-FUNCTIONSPublished online by Cambridge University Press: 22 February 2022
In this paper, we study lower-order terms of the one-level density of low-lying zeros of quadratic Hecke L-functions in the Gaussian field. Assuming the generalized Riemann hypothesis, our result is valid for even test functions whose Fourier transforms are supported in
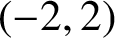 $(-2, 2)$
. Moreover, we apply the ratios conjecture of L-functions to derive these lower-order terms as well. Up to the first lower-order term, we show that our results are consistent with each other when the Fourier transforms of the test functions are supported in
$(-2, 2)$
. Moreover, we apply the ratios conjecture of L-functions to derive these lower-order terms as well. Up to the first lower-order term, we show that our results are consistent with each other when the Fourier transforms of the test functions are supported in
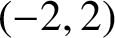 $(-2, 2)$
.
$(-2, 2)$
.
Communicated by Dzmitry Badziahin
P. G. is supported in part by NSFC grant 11871082 and L. Z. by FRG grant PS43707 and the Goldstar Award PS53450 from the University of New South Wales (UNSW). Parts of this work were done when P. G. visited UNSW in September 2019. He wishes to thank UNSW for the invitation, financial support and warm hospitality during his pleasant stay. Finally, the authors thank the anonymous referee for his/her very careful reading of this manuscript and many helpful comments and suggestions.