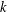 $k$TH YAU NUMBER OF ISOLATED HYPERSURFACE SINGULARITIES AND AN INEQUALITY CONJECTURE
$k$TH YAU NUMBER OF ISOLATED HYPERSURFACE SINGULARITIES AND AN INEQUALITY CONJECTUREPublished online by Cambridge University Press: 30 April 2019
Let 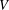 $V$ be a hypersurface with an isolated singularity at the origin defined by the holomorphic function
$V$ be a hypersurface with an isolated singularity at the origin defined by the holomorphic function 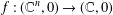 $f:(\mathbb{C}^{n},0)\rightarrow (\mathbb{C},0)$. The Yau algebra
$f:(\mathbb{C}^{n},0)\rightarrow (\mathbb{C},0)$. The Yau algebra 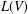 $L(V)$ is defined to be the Lie algebra of derivations of the moduli algebra
$L(V)$ is defined to be the Lie algebra of derivations of the moduli algebra 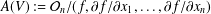 $A(V):={\mathcal{O}}_{n}/(f,\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}x_{1},\ldots ,\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}x_{n})$, that is,
$A(V):={\mathcal{O}}_{n}/(f,\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}x_{1},\ldots ,\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}x_{n})$, that is, 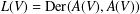 $L(V)=\text{Der}(A(V),A(V))$. It is known that
$L(V)=\text{Der}(A(V),A(V))$. It is known that 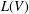 $L(V)$ is finite dimensional and its dimension
$L(V)$ is finite dimensional and its dimension 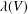 $\unicode[STIX]{x1D706}(V)$ is called the Yau number. We introduce a new series of Lie algebras, that is,
$\unicode[STIX]{x1D706}(V)$ is called the Yau number. We introduce a new series of Lie algebras, that is, 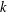 $k$th Yau algebras
$k$th Yau algebras 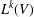 $L^{k}(V)$,
$L^{k}(V)$, 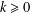 $k\geq 0$, which are a generalization of the Yau algebra. The algebra
$k\geq 0$, which are a generalization of the Yau algebra. The algebra 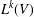 $L^{k}(V)$ is defined to be the Lie algebra of derivations of the
$L^{k}(V)$ is defined to be the Lie algebra of derivations of the 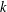 $k$th moduli algebra
$k$th moduli algebra 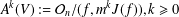 $A^{k}(V):={\mathcal{O}}_{n}/(f,m^{k}J(f)),k\geq 0$, that is,
$A^{k}(V):={\mathcal{O}}_{n}/(f,m^{k}J(f)),k\geq 0$, that is, 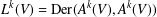 $L^{k}(V)=\text{Der}(A^{k}(V),A^{k}(V))$, where
$L^{k}(V)=\text{Der}(A^{k}(V),A^{k}(V))$, where  $m$ is the maximal ideal of
$m$ is the maximal ideal of 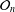 ${\mathcal{O}}_{n}$. The
${\mathcal{O}}_{n}$. The 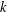 $k$th Yau number is the dimension of
$k$th Yau number is the dimension of 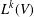 $L^{k}(V)$, which we denote by
$L^{k}(V)$, which we denote by 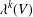 $\unicode[STIX]{x1D706}^{k}(V)$. In particular,
$\unicode[STIX]{x1D706}^{k}(V)$. In particular, 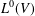 $L^{0}(V)$ is exactly the Yau algebra, that is,
$L^{0}(V)$ is exactly the Yau algebra, that is, 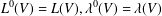 $L^{0}(V)=L(V),\unicode[STIX]{x1D706}^{0}(V)=\unicode[STIX]{x1D706}(V)$. These numbers
$L^{0}(V)=L(V),\unicode[STIX]{x1D706}^{0}(V)=\unicode[STIX]{x1D706}(V)$. These numbers 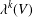 $\unicode[STIX]{x1D706}^{k}(V)$ are new numerical analytic invariants of singularities. In this paper we formulate a conjecture that
$\unicode[STIX]{x1D706}^{k}(V)$ are new numerical analytic invariants of singularities. In this paper we formulate a conjecture that 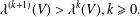 $\unicode[STIX]{x1D706}^{(k+1)}(V)>\unicode[STIX]{x1D706}^{k}(V),k\geq 0.$ We prove this conjecture for a large class of singularities.
$\unicode[STIX]{x1D706}^{(k+1)}(V)>\unicode[STIX]{x1D706}^{k}(V),k\geq 0.$ We prove this conjecture for a large class of singularities.
Communicated by F. Larusson
Both S. Yau and H. Zuo were supported by NSFC Grant 11531007 and the start-up fund from Tsinghua University. H. Zuo was also supported by NSFC Grant 11771231 and the Tsinghua University Initiative Scientific Research Program.