Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T13:57:59.215Z Has data issue: false hasContentIssue false
  • English
  • Français

DIRICHLET FORMS AND ULTRAMETRIC CANTOR SETS ASSOCIATED TO HIGHER-RANK GRAPHS

Part of: Selfadjoint operator algebras Markov processes

Published online by Cambridge University Press:  08 January 2020

JAESEONG HEO Open the ORCID record for JAESEONG HEO [Opens in a new window] ,
SOORAN KANG Open the ORCID record for SOORAN KANG [Opens in a new window]  and
YONGDO LIM
JAESEONG HEO
Affiliation:
Department of Mathematics, Research Institute for Natural Sciences,Hanyang University, Seoul, 04763, Republic of Korea e-mail: [email protected]
SOORAN KANG*
Affiliation:
College of General Education,Chung-Ang University, Seoul, 06974, Republic of Korea
YONGDO LIM
Affiliation:
Department of Mathematics,Sungkyunkwan University, Suwon, 16419, Republic of Korea e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The aim of this paper is to study the heat kernel and the jump kernel of the Dirichlet form associated to the ultrametric Cantor set 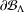$\unicode[STIX]{x2202}{\mathcal{B}}_{\unicode[STIX]{x1D6EC}}$ that is the infinite path space of the stationary 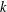$k$-Bratteli diagram 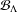${\mathcal{B}}_{\unicode[STIX]{x1D6EC}}$, where 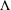$\unicode[STIX]{x1D6EC}$ is a finite strongly connected 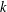$k$-graph. The Dirichlet form which we are interested in is induced by an even spectral triple 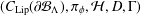$(C_{\operatorname{Lip}}(\unicode[STIX]{x2202}{\mathcal{B}}_{\unicode[STIX]{x1D6EC}}),\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D719}},{\mathcal{H}},D,\unicode[STIX]{x1D6E4})$ and is given by

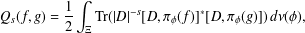$$\begin{eqnarray}Q_{s}(f,g)=\frac{1}{2}\int _{\unicode[STIX]{x1D6EF}}\operatorname{Tr}(|D|^{-s}[D,\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D719}}(f)]^{\ast }[D,\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D719}}(g)])\,d\unicode[STIX]{x1D708}(\unicode[STIX]{x1D719}),\end{eqnarray}$$
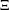where $\unicode[STIX]{x1D6EF}$ is the space of choice functions on 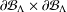$\unicode[STIX]{x2202}{\mathcal{B}}_{\unicode[STIX]{x1D6EC}}\times \unicode[STIX]{x2202}{\mathcal{B}}_{\unicode[STIX]{x1D6EC}}$. There are two ultrametrics, 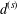$d^{(s)}$ and 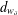$d_{w_{\unicode[STIX]{x1D6FF}}}$, on 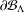$\unicode[STIX]{x2202}{\mathcal{B}}_{\unicode[STIX]{x1D6EC}}$ which make the infinite path space 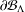$\unicode[STIX]{x2202}{\mathcal{B}}_{\unicode[STIX]{x1D6EC}}$ an ultrametric Cantor set. The former 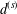$d^{(s)}$ is associated to the eigenvalues of the Laplace–Beltrami operator 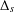$\unicode[STIX]{x1D6E5}_{s}$ associated to 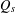$Q_{s}$, and the latter 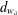$d_{w_{\unicode[STIX]{x1D6FF}}}$ is associated to a weight function 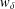$w_{\unicode[STIX]{x1D6FF}}$ on 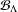${\mathcal{B}}_{\unicode[STIX]{x1D6EC}}$, where 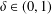$\unicode[STIX]{x1D6FF}\in (0,1)$. We show that the Perron–Frobenius measure 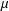$\unicode[STIX]{x1D707}$ on 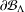$\unicode[STIX]{x2202}{\mathcal{B}}_{\unicode[STIX]{x1D6EC}}$ has the volume-doubling property with respect to both 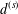$d^{(s)}$ and 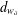$d_{w_{\unicode[STIX]{x1D6FF}}}$ and we study the asymptotic behavior of the heat kernel associated to 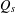$Q_{s}$. Moreover, we show that the Dirichlet form 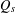$Q_{s}$ coincides with a Dirichlet form 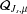${\mathcal{Q}}_{J_{s},\unicode[STIX]{x1D707}}$ which is associated to a jump kernel 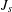$J_{s}$ and the measure 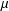$\unicode[STIX]{x1D707}$ on 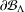$\unicode[STIX]{x2202}{\mathcal{B}}_{\unicode[STIX]{x1D6EC}}$, and we investigate the asymptotic behavior and moments of displacements of the process.

Keywords

Dirichlet formsk-graphs and k-Bratteli diagramsheat kernelsasymptotic behaviorsultrametric Cantor sets

MSC classification

Primary: 46L87: Noncommutative differential geometry
Secondary: 60J75: Jump processes
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 110 , Issue 2 , April 2021 , pp. 194 - 219
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by A. Sims

The first author J.H. and the third author Y.L. were supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MEST), No. NRF-2015R1A3A2031159. The second author S.K. was supported by the Basic Science Research Program through a NRF grant funded by the Ministry of Education, No. NRF-2017R1D1A1B03034697.

References

Abe, M. and Kawamura, K., ‘Branching laws for endomorphisms of fermions and the Cuntz algebra 𝓞2’, J. Math. Phys. 49 (2008), 043501, 10 pp.Google Scholar
Bezuglyi, S. and Jorgensen, P. E. T., ‘Representations of Cuntz–Krieger relations, dynamics on Bratteli diagrams, and path-space measures’, in: Trends in Harmonic Analysis and its Applications, Contemporary Mathematics, 650 (American Mathematical Society, Providence, RI, 2015), 57–88.Google Scholar
Carlsen, T., Kang, S., Shotwell, J. and Sims, A., ‘The primitive ideals of the Cuntz–Krieger algebra of a row-finite higher-rank graph with no sources’, J. Funct. Anal. 266 (2014), 2570–2589.Google Scholar
Chen, Z.-Q. and Kumagai, T., ‘Heat kernel estimates for jump processes of mixed types on metric measure space’, Probab. Theory Related Fields 140 (2008), 277–317.Google Scholar
Davidson, K. R. and Yang, D., ‘Periodicity in rank 2 graph algebras’, Canad. J. Math. 61 (2009), 1239–1261.Google Scholar
Dutkay, D. E. and Jorgensen, P. E. T., ‘Analysis of orthogonality and of orbits in affine iterated function systems’, Math. Z. 256(4) (2007), 801–823.Google Scholar
Evans, D. G., ‘On the K-theory of higher rank graph C ∗ -algebras’, New York J. Math. 14 (2008), 1–31.Google Scholar
Farsi, C., Gillaspy, E., Jorgensen, P., Kang, S. and Packer, J., ‘Representations of higher-rank graph C ∗ -algebras associated to 𝛬-semibranching function systems’, J. Math. Anal. Appl. 488 (2018), 766–798.Google Scholar
Farsi, C., Gillaspy, E., Jorgensen, P., Kang, S. and Packer, J., ‘Monic representations of finite higher-rank graphs’, Ergod. Th. & Dynam. Sys., to appear. Published online (6 September 2018).Google Scholar
Farsi, C., Gillaspy, E., Julien, A., Kang, S. and Packer, J., ‘Wavelets and spectral triples for fractal representations of Cuntz algebras’, in: Problems and Recent Methods in Operator Theory, Contemporary Mathematics, 687 (American Mathematical Society, Providence, RI, 2017), 103–133.Google Scholar
Farsi, C., Gillaspy, E., Julien, A., Kang, S. and Packer, J., ‘Spectral triples and wavelets for higher-rank graphs’, J. Math. Anal. Appl., to appear.Google Scholar
Farsi, C., Gillaspy, E., Kang, S. and Packer, J., ‘Separable representations, KMS states, and wavelets for higher-rank graphs’, J. Math. Anal. Appl. 434 (2015), 241–270.Google Scholar
Fukushima, M., Oshima, Y. and Takeda, M., Dirichlet Forms and Symmetric Markov Processes, de Gruyter Studies in Mathematics, 19 (de Gruyter, Berlin, 1994).Google Scholar
an Huef, A., Laca, M., Raeburn, I. and Sims, A., ‘KMS states on the C ∗ -algebra of a higher-rank graph and periodicity in the path space’, J. Funct. Anal. 268 (2015), 1840–1875.Google Scholar
Julien, A. and Savinien, J., ‘Transverse Laplacians for substitution tiling’, Comm. Math. Phys. 301 (2011), 285–318.Google Scholar
Kigami, J., ‘Dirichlet forms and associated heat kernels on the Cantor set induced by random walks on trees’, Adv. Math. 225 (2010), 2674–2730.Google Scholar
Kumjian, A. and Pask, D., ‘Higher rank graph C ∗ -algebras’, New York J. Math. 6 (2000), 1–20.Google Scholar
Marcolli, M. and Paolucci, A. M., ‘Cuntz–Krieger algebras and wavelets on fractals’, Complex Anal. Oper. Theory 5 (2011), 41–81.Google Scholar
Pearson, J. and Bellissard, J., ‘Noncommutative Riemannian geometry and diffusion on ultrametric Cantor sets’, J. Noncommut. Geom. 3 (2009), 447–480.Google Scholar
Ruiz, E., Sims, A. and Sørensen, A. P. W., ‘UCT-Kirchberg algebras have nuclear dimension one’, Adv. Math. 279 (2015), 1–28.Google Scholar