Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-04-24T16:55:43.134Z Has data issue: false hasContentIssue false
  • English
  • Français

COMMON ZEROS OF IRREDUCIBLE CHARACTERS

Part of: Representation theory of groups

Published online by Cambridge University Press:  11 December 2023

NGUYEN N. HUNG Open the ORCID record for NGUYEN N. HUNG [Opens in a new window] ,
ALEXANDER MORETÓ  and
LUCIA MOROTTI
NGUYEN N. HUNG*
Affiliation:
Department of Mathematics, The University of Akron, Akron, OH 44325, USA
ALEXANDER MORETÓ
Affiliation:
Departamento de Matemáticas, Universidad de Valencia, 46100 Burjassot, Valencia, Spain e-mail: [email protected]
LUCIA MOROTTI
Affiliation:
Mathematisches Institut, Heinrich-Heine-Universität Düsseldorf, 40225 Düsseldorf, Germany e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the zero-sharing behavior among irreducible characters of a finite group. For symmetric groups 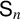$\mathsf {S}_n$, it is proved that, with one exception, any two irreducible characters have at least one common zero. To further explore this phenomenon, we introduce the common-zero graph of a finite group G, with nonlinear irreducible characters of G as vertices, and edges connecting characters that vanish on some common group element. We show that for solvable and simple groups, the number of connected components of this graph is bounded above by three. Lastly, the result for 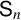$\mathsf {S}_n$ is applied to prove the nonequivalence of the metrics on permutations induced from faithful irreducible characters of the group.

Keywords

zeros of charactersirreducible characters

MSC classification

Primary: 20C15: Ordinary representations and characters
Secondary: 20C30: Representations of finite symmetric groups 20D06: Simple groups 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 117 , Issue 2 , October 2024 , pp. 105 - 129
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The second author thanks Noelia Rizo for helpful conversations. The authors also thank Silvio Dolfi for checking one result. The first author is grateful for the support of the UA Faculty Research Grant FRG 1747. The research of the second author is supported by Ministerio de Ciencia e Innovación (Grants PID2019-103854GB-I00 and PID2022-137612NB-I00 funded by MCIN/AEI/10.13039/501100011033 and ‘ERDF A way of making Europe’) and Generalitat Valenciana CIAICO/2021/163. While working on the revised version the third author was working at the Department of Mathematics of the University of York, supported by the Royal Society grant URF$\setminus$R$\setminus$221047.

Communicated by Michael Giudici

References

Bubboloni, D., Dolfi, S. and Spiga, P., ‘Finite groups whose irreducible characters vanish only on $p$ -elements’, J. Pure Appl. Algebra 213 (2009), 370–376.CrossRefGoogle Scholar
Carter, R. W., Finite Groups of Lie Type. Conjugacy Classes and Complex Characters (Wiley and Sons, New York, 1985).Google Scholar
Deza, M. M. and Deza, E., Encyclopedia of Distances, 2nd edn (Springer, Berlin–Heidelberg, 2013).CrossRefGoogle Scholar
Diaconis, P., Group Representations in Probability and Statistics, Institute of Mathematical Statistics Lecture Notes–Monograph Series, 11 (Institute of Mathematical Statistics, Hayward, CA, 1988).CrossRefGoogle Scholar
Digne, F. and Michel, J., Representations of Finite Groups of Lie Type, London Mathematical Society Student Texts 21 (Cambridge University Press, Cambridge, 1991).CrossRefGoogle Scholar
Dolfi, S., Pacifici, E. and Sanus, L., ‘On zeros of characters of finite groups’, in: Group Theory and Computation, Indian Statistical Institute Series (eds. Sastry, N. and Yadav, M.) (Springer, Singapore, 2018), 41–58.CrossRefGoogle Scholar
Gallagher, P. X., Larsen, M. J. and Miller, A. R., ‘Many zeros of many characters of $\mathrm{GL}\left(n,q\right)$ $^{\prime }$ , Int. Math. Res. Not. IMRN 6 (2022), 4376–4386.CrossRefGoogle Scholar
GAP Group, GAP Groups, algorithms, and programming, version 4.12.1, 2022. http://www.gap-system.org.Google Scholar
Granville, A. and Ono, K., ‘Defect zero $p$ -blocks for finite simple groups’, Trans. Amer. Math. Soc. 348 (1996), 331–347.CrossRefGoogle Scholar
Hanaki, A. and Okuyama, T., ‘Groups with some combinatorial properties’, Osaka J. Math. 34 (1997), 337–356.Google Scholar
Hung, N. N., ‘The continuity of $p$ -rationality and a lower bound for ${p}^{\prime }$ -degree irreducible characters of finite groups’, Trans. Amer. Math. Soc., to appear, arXiv:2205.15899.Google Scholar
Isaacs, I. M., Character Theory of Finite Groups (AMS-Chelsea, Providence, RI, 2006).Google Scholar
Isaacs, I. M., Navarro, G. and Wolf, T. R., ‘Finite group elements where no irreducible character vanishes’, J. Algebra 222 (1999), 413–423.CrossRefGoogle Scholar
James, G. and Kerber, A., The Representation Theory of the Symmetric Group, Encyclopedia of Mathematics and Its Applications, 16 (Addison-Wesley Publishing Co., Reading, MA, 1981).Google Scholar
James, G. D., The Representation Theory of the Symmetric Groups, Lecture Notes in Mathematics, 682 (Springer, New York–Heidelberg–Berlin, 1978).CrossRefGoogle Scholar
Larsen, M. J. and Miller, A. R., ‘The sparsity of character tables of high rank groups of Lie type’, Represent. Theory 25 (2021), 173–192.CrossRefGoogle Scholar
Lewis, M. L., ‘Solvable groups whose degree graphs have two connected components’, J. Group Theory 4 (2001), 255–275.CrossRefGoogle Scholar
Lewis, M. L., ‘An overview of graphs associated with character degrees and conjugacy class sizes of finite groups’, Rocky Mountain J. Math. 38 (2008), 175–211.CrossRefGoogle Scholar
Lewis, M. L. and White, D. L., ‘Connectedness of degree graphs of non-solvable groups’, J. Algebra 266 (2003), 51–76.CrossRefGoogle Scholar
Lübeck, F. and Malle, G., ‘(2,3)-Generation of exceptional groups’, J. Lond. Math. Soc. (2) 59 (1999), 109–122.CrossRefGoogle Scholar
Malle, G., ‘Almost irreducible tensor squares’, Comm. Algebra 27 (1999), 1033–1051.CrossRefGoogle Scholar
Malle, G., Navarro, G. and Olsson, J., ‘Zeros of characters of finite groups’, J. Group Theory 3 (2000), 353–368.CrossRefGoogle Scholar
Malle, G., Saxl, J. and Weigel, T., ‘Generation of classical groups’, Geom. Dedicata 49 (1994), 85–116.CrossRefGoogle Scholar
Malle, G. and Testerman, D., Linear Algebraic Groups and Finite Groups of Lie Type, Cambridge Studies in Advanced Mathematics, 133 (Cambridge University Press, Cambridge, 2011).CrossRefGoogle Scholar
Manz, O., Staszewski, R. and Willems, W., ‘On the number of components of a graph related to character degrees’, Proc. Amer. Math. Soc. 103 (1988), 31–37.CrossRefGoogle Scholar
Manz, O. and Wolf, T. R., Representations of Solvable Groups (Cambridge University Press, Cambridge, 1993).CrossRefGoogle Scholar
McSpirit, E. and Ono, K., ‘Zeros in the character tables of symmetric groups with an $l$ -core index’, Canad. Math. Bull. 66 (2023), 467–476.CrossRefGoogle Scholar
Miller, A. R., ‘The probability that a character value is zero for the symmetric group’, Math. Z. 277 (2014), 1011–1015.CrossRefGoogle Scholar
Moretó, A. and Sangroniz, J., ‘On the number of conjugacy classes of zeros of characters’, Israel J. Math. 142 (2004), 163–187.CrossRefGoogle Scholar
Moretó, A. and Wolf, T. R., ‘Orbit sizes, character degrees and Sylow subgroups’, Adv. Math. 184 (2004), 18–36.CrossRefGoogle Scholar
Morotti, L., ‘On multisets of hook lengths of partitions’, Discrete Math. 313 (2013), 2792–2797.CrossRefGoogle Scholar
Morotti, L., ‘Explicit construction of universal sampling sets for finite abelian and symmetric groups’, PhD Thesis, RWTH-Aachen University, 2014.Google Scholar
Navarro, G., Character Theory and the McKay Conjecture, Cambridge Studies in Advanced Mathematics, 175 (Cambridge University Press, Cambridge, 2018).CrossRefGoogle Scholar
Nguyen, H. N., ‘Low-dimensional complex characters of the symplectic and orthogonal groups’, Comm. Algebra 38 (2010), 1157–1197.CrossRefGoogle Scholar
Peluse, S. and Soundararajan, K., ‘Almost all entries in the character table of the symmetric group are multiples of any given prime’, J. reine angew. Math. 786 (2022), 45–53.CrossRefGoogle Scholar
Podesta, R. and Vides, M. G., ‘Invariant metrics on finite groups’, Discrete Math. 346 (2023), Article no. 113194, 28 pages.CrossRefGoogle Scholar
Wolf, T. R., ‘Character correspondences in solvable groups’, Illinois J. Math. 22 (1978), 327–340.CrossRefGoogle Scholar
Yang, Y., ‘Orbits of the actions of finite solvable groups’, J. Algebra 321 (2009), 2012–2021.CrossRefGoogle Scholar