Published online by Cambridge University Press: 24 July 2020
Let 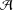 ${\mathcal{A}}$ be a semisimple Banach algebra with minimal left ideals and
${\mathcal{A}}$ be a semisimple Banach algebra with minimal left ideals and 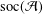 $\text{soc}({\mathcal{A}})$ be the socle of
$\text{soc}({\mathcal{A}})$ be the socle of 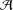 ${\mathcal{A}}$. We prove that if
${\mathcal{A}}$. We prove that if 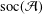 $\text{soc}({\mathcal{A}})$ is an essential ideal of
$\text{soc}({\mathcal{A}})$ is an essential ideal of 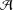 ${\mathcal{A}}$, then every 2-local derivation on
${\mathcal{A}}$, then every 2-local derivation on 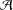 ${\mathcal{A}}$ is a derivation. As applications of this result, we can easily show that every 2-local derivation on some algebras, such as semisimple modular annihilator Banach algebras, strongly double triangle subspace lattice algebras and
${\mathcal{A}}$ is a derivation. As applications of this result, we can easily show that every 2-local derivation on some algebras, such as semisimple modular annihilator Banach algebras, strongly double triangle subspace lattice algebras and 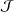 ${\mathcal{J}}$-subspace lattice algebras, is a derivation.
${\mathcal{J}}$-subspace lattice algebras, is a derivation.
Communicated by A. Sims
This paper was partially supported by the National Natural Science Foundation of China (Grant No. 11871021).