Zu jedem Zählausdruck A in der allgemeinen pränexen Normalform

kann man bekanntlich einen, in bezug auf die Erfüllbarkeit, gleichwertigen Zählausdruck B in der spezielleren Normalform (Skolemsche Nonnalfonn)

konstruieren, indem man auf A mehrmals (n–1 Mal) das sogenannte Skolemsche Verfahren anwendet. Dieses Verfahren hat nämlich die Eigenschaft, daß es auf einen Zählausdruck in der pränexen Normalform n-ten Grades (n > 1) angewandt zu einem gleichwertigen Zählausdruck in der pränexen Normalform (n–1)-ten Grades führt, wobei unter “Grad eines Zählausdrucks in der pränexen Normalform, die ein mit einem Allzeichen beginnendes und mit einem Seinszeichen endendes Präfix hat” die Anzahl der durch Seinszeichen voneinander getrennten Komplexe von Allzeichen dieses Präfixes zu verstehen ist. Da nun A—wie aus (1) ersichtlich ist—ein Zählausdruck n-ten Grades ist, so kommt man nach (n–1)-maliger Anwendung des Skolemschen Verfahrens tatsächlich zu einem gleichwertigen Zählausdruck ersten Grades, also zu einem gleichwertigen Zählausdruck der Form (2).

In Oskar Becker's Zur Logik der Modalitäten four systems of modal logic are considered. Two of these are mentioned in Appendix II of Lewis and Langford's Symbolic logic. The first system is based on A1–8 plus the postulate,

From A7: ∼◊p⊰∼p we can prove the converse of C11 by writing ∼◊p for p, and hence derive

The addition of this postulate to A1–8, as Becker points out, allows us to “reduce” all complex modal functions to six, and these six are precisely those which Lewis mentions in his postulates and theorems: p, ∼p, ◊p, ∼◊p, ∼◊∼p, and ◊∼p This reduction is accomplished by showing

where ◊n means that the modal operator ◊ is repeated n times; e.g., ◊3p = ◊◊◊p. Then it is shown that

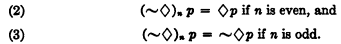
By means of (1), (2), and (3) any complex modal function whatsoever may be reduced to one of the six “simple” modals mentioned above.

It might be asked whether this reduction could be carried out still further, i.e., whether two of the six “irreducible” modals could not be equated. But such a reduction would have to be based on the fact that ◊p = p which is inconsistent with the set B1–9 of Lewis and Langford's Symbolic logic and independent of the set A1–8. Hence for neither set would such a reduction be possible.