Friedberg [3] showed that every degree of unsolvability above 0′ is the jump of some degree, and Sacks [9] showed that the degrees above 0′ which are recursively enumerable (r.e.) in 0′ are the jumps of the r.e. degrees.
In this paper we examine the extent to which the Sacks jump theorem can be combined with the minimal pair theorem of Lachlan [4] and Yates [13]. We prove below that there is a degree c > 0′ which is r.e. in 0′ but which is not the jump of half a minimal pair of r.e. degrees.
This extends Yates' result [13] proving the existence of noncappable degrees (that is, r.e. degrees a < 0′ for which there is no corresponding r.e. b > 0 with a ∩ b = 0).
It also throws more light on the class PS of promptly simple degrees. It was shown by Ambos-Spies, Jockusch, Shore and Soare [1] that PS coincides with the class NC of noncappable degrees, and with the class LC of all low-cuppable degrees, and (using earlier work of Maass, Shore and Stob [5]) that PS splits every class Hn or Ln, n ≥ 0, in the high-low hierarchy of r.e. degrees.
If c > 0′, with c r.e. in 0′, let
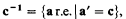
and call c−1 the jump class for c. It is easy to see that every jump class contains members of PS (= NC = LC). By Sacks [8] there exists a low a ∈ LC, where of course [a, 0′] (= {br.e. ∣a ≤ b ≤ 0′}) ⊆ LC = PS. But by Robinson [7] [a, 0′] intersects with every jump class.
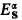 -arithmetic
-arithmetic