Research Article
A simplification of combinatory logic1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 225-246
-
- Article
- Export citation
On models with power-like orderings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 247-267
-
- Article
- Export citation
Ramsey's theorem and recursion theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 268-280
-
- Article
- Export citation
Ordinal recursion, and a refinement of the extended Grzegorczyk hierarchy
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 281-292
-
- Article
- Export citation
Existentially closed structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 293-310
-
- Article
- Export citation
Which number theoretic problems can be solved in recursive progressions on Π11-paths through O?
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 311-334
-
- Article
- Export citation
Some model theory of abelian groups
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 335-342
-
- Article
- Export citation
Generalized interpolation theorems
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 343-351
-
- Article
- Export citation
A reduction theorem for predicate logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 352-354
-
- Article
- Export citation
A system of abstract constructive ordinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 355-374
-
- Article
- Export citation
Sufficient conditions for the undecidability of intuitionistic theories with applications1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 375-384
-
- Article
- Export citation
General models, descriptions, and choice in type theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 385-394
-
- Article
- Export citation
General models and extensionality
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 395-397
-
- Article
- Export citation
Reviews
Richard T. Cox. Probability, frequency and reasonable expectation. American journal of physics, vol. 14 (1946), pp. 1–13. - Richard T. Cox. The algebra of probable inference. The Johns Hopkins Press, Baltimore1961, x + 114 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 398-399
-
- Article
- Export citation
R. Engelking and K. Kuratowski. Quelques théorèmes de l'algèbre de Boole et leurs applications topologiques. Fundamenta mathematicae, vol. 50 (1962), pp. 519–535.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 399-400
-
- Article
- Export citation
F. E. J. Linton. Injective Boolean σ-algebras. Archiv der Mathematik, vol. 17 (1966), pp. 383–387.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 400
-
- Article
- Export citation
J. Donald Monk. Nontrivial -injective Boolean algebras do not exist. Bulletin of the American Mathematical Society, vol. 73 (1967), pp. 526–527.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 400
-
- Article
- Export citation
S. R. Kogalovskij. Ob univérsal'nyh klassah algébr (On universal classes of algebras). Doklady Akadémii Nauk SSSR, vol. 122 (1958), pp. 759–761.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 400-401
-
- Article
- Export citation
S. R. Kogalovskij. O kvaziproéktivnyh klassah modéléj. Russian original of XXXVII 428. (On universal classes of algebras). Doklady Akadémii Nauk SSSR, vol. 148 (1963), pp. 505–507.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 401
-
- Article
- Export citation
S. R. Kogalovskij. Strukturnyé haraktéristiki universal'nyh klassov (Structural characteristics of universal classes). Sibirskij matématičéskij žurnal, vol. 4 (1963), pp. 97–119.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 401-402
-
- Article
- Export citation

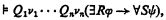
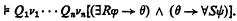


 of A in ℳ. Hintikka points out in [10, p. 3] that this constitutes a rather strong requirement concerning the structure of a general model. Henkin draws attention to the problem of constructing nonstandard models for the theory of types in [9, p. 324].
of A in ℳ. Hintikka points out in [10, p. 3] that this constitutes a rather strong requirement concerning the structure of a general model. Henkin draws attention to the problem of constructing nonstandard models for the theory of types in [9, p. 324]. , i.e.,
, i.e.,  as an axiom schema.
as an axiom schema.