Research Article
Theories of arithmetics in finite models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-28
-
- Article
- Export citation
Model completeness of o-minimal structures expanded by Dedekind cuts
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 29-60
-
- Article
- Export citation
Generic substitutions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 61-83
-
- Article
- Export citation
The finite model property for knotted extensions of propositional linear logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 84-98
-
- Article
- Export citation
Derivations of the Frobenius map
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 99-110
-
- Article
- Export citation
The computable dimension of trees of infinite height
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 111-141
-
- Article
- Export citation
Subsets of superstable structures are weakly benign
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 142-150
-
- Article
- Export citation
Computable categoricity of trees of finite height
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 151-215
-
- Article
- Export citation
On Kueker simple theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 216-222
-
- Article
- Export citation
Interpolation for extended modal languages
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 223-234
-
- Article
- Export citation
On the weak non-finite cover property and the n-tuples of simple structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 235-251
-
- Article
- Export citation
On the definable ideal generated by nonbounding c.e. degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 252-270
-
- Article
- Export citation
Fusing o-minimal structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 271-281
-
- Article
- Export citation
On an algebra of lattice-valued logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 282-318
-
- Article
- Export citation
Relative randomness and real closed fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 319-330
-
- Article
- Export citation
The isomorphism problem for computable Abelian p-groups of bounded length
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 331-345
-
- Article
- Export citation
On relatively analytic and Borel subsets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 346-352
-
- Article
- Export citation
Front matter
JSL Volume 70 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JSL Volume 70 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation

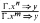 . It is proved that the class of algebraic models for such a logic has the
. It is proved that the class of algebraic models for such a logic has the 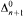 -condition. We show that all trees which are not computably categorical have computable dimension ω. Finally, we prove that for every
-condition. We show that all trees which are not computably categorical have computable dimension ω. Finally, we prove that for every  to be the smallest cardinality of a function
to be the smallest cardinality of a function