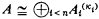Research Article
One hundred and two problems in mathematical logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 113-129
-
- Article
- Export citation
A survey of partial degrees1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 130-140
-
- Article
- Export citation
The inadequacy of the neighbourhood semantics for modal logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 141-148
-
- Article
- Export citation
Sets equipollent to their power set in NF
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 149-150
-
- Article
- Export citation
Natural models and Ackermann-type set theories1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 151-158
-
- Article
- Export citation
Independent Gödel sentences and independent sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 159-166
-
- Article
- Export citation
An algebraic characterization of power set in countable standard models of ZF1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 167-170
-
- Article
- Export citation
A simplification of the Bachmann method for generating large countable ordinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 171-185
-
- Article
- Export citation
On spectra, and the negative solution of the decision problem for identities having a finite nontrivial model1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 186-196
-
- Article
- Export citation
Two forms of the axiom of choice for an elementary topos
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 197-212
-
- Article
- Export citation
ℵ0-categorical modules
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 213-220
-
- Article
- Export citation
Extending Gödel's negative interpretation to ZF
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 221-229
-
- Article
- Export citation
Reviews
G. Kreisel. Some reasons for generalizing recursion theory. Logic colloquium '69, Proceedings of the summer school and colloquium in mathematical logic, Manchester, August 1969, edited by R. O. Gandy and C. E. M. Yates, Studies in logic and the foundations of mathematics, vol. 61, North-Holland Publishing Company, Amsterdam and London1971, pp. 139–198.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 230-232
-
- Article
- Export citation
Dag Prawitz. Ideas and results in proof theory. Proceedings of the Second Scandinavian Logic Symposium, edited by J. E. Fenstad, Studies in logic and the foundations of mathematics, vol. 63, North-Holland Publishing Company, Amsterdam and London1971, pp. 235–307.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 232-234
-
- Article
- Export citation
Joseph R. Shoenfield. Mathematical logic. Addison-Wesley Publishing Company, Reading, Mass., Menlo Park, Calif., London, and Don Mills, Ontario, 1967, viii + 344 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 234-236
-
- Article
- Export citation
Maria Luisa Dalla Chiara Scabia. Modelli sintattici e semantici delle teorie elementari. Feltrinelli Editore, Milan1968, 240 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 236-237
-
- Article
- Export citation
Raymond M. Smullyan. First-order logic. Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 43, Springer-Verlag, Berlin, Heidelberg, and New York, 1968, XII + 158 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 237-238
-
- Article
- Export citation
Jean-Pierre Bénéjam. Application du théorème de Herbrand à la présentation de thèses tératologiques du calcul des prédicats élémentaire. Comptes rendus hebdomadaires des séances de l'Académie des Sciences, ser. A vol. 268 (1969), pp. 757–760. - Roland Fraïssé. Réflexions sur la complétude selon Herbrand. International logic review-Rassegna internazionale di logica (Bologna), vol. 3 no. 1 (1972), pp. 86–98.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 238-239
-
- Article
- Export citation
Wilbur John WalkoeJr., Finite partially-ordered quantification. The journal of symbolic logic, vol. 35 (for 1970, pub. 1971), pp. 535–555.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 239-240
-
- Article
- Export citation
Donald Monk. Singulary cylindric and polyadic equality algebras. Transactions of the American Mathematical Society, vol. 112 (1964), pp. 185–205.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 240
-
- Article
- Export citation

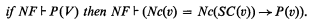
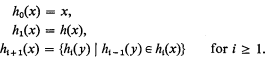
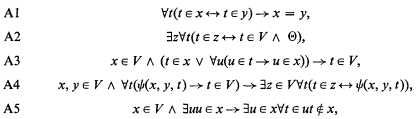
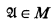 is a countable (in
is a countable (in 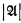 ) subsets of
) subsets of 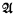 is isomorphic to the power set algebra of Λ in
is isomorphic to the power set algebra of Λ in 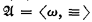 and
and 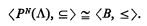
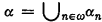 . Indeed this was the motivation for Bachmann's original construction. However the initial segments
. Indeed this was the motivation for Bachmann's original construction. However the initial segments 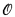 (the language of groupoids), the set of identities
(the language of groupoids), the set of identities 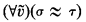 that have no nontrivial model, is recursively inseparable from the set of identities
that have no nontrivial model, is recursively inseparable from the set of identities 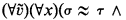
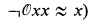 has a finite model. As a corollary, we have that each of the following problems, restricted to sentences defined in the language of groupoids, is algorithmically unsolvable: (1) to decide if an identity has a finite nontrivial model; (2) to decide if an identity has a nontrivial model; (3) to decide if a universal sentence has a finite model; (4) to decide if a universal sentence has a model. We note that the undecidability of (2) was proved earlier by McNulty [13, Theorem 3.6(i)], improving results obtained by Murskiǐ [14] and by Perkins [17]. The other parts of the corollary seem to be new.
has a finite model. As a corollary, we have that each of the following problems, restricted to sentences defined in the language of groupoids, is algorithmically unsolvable: (1) to decide if an identity has a finite nontrivial model; (2) to decide if an identity has a nontrivial model; (3) to decide if a universal sentence has a finite model; (4) to decide if a universal sentence has a model. We note that the undecidability of (2) was proved earlier by McNulty [13, Theorem 3.6(i)], improving results obtained by Murskiǐ [14] and by Perkins [17]. The other parts of the corollary seem to be new.