Research Article
An application of nonstandard analysis to game theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 385-394
-
- Article
- Export citation
On measures on complete Boolean algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 395-406
-
- Article
- Export citation
Elementary embeddings and infinitary combinatorics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 407-413
-
- Article
- Export citation
Resolution in type theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 414-432
-
- Article
- Export citation
A splitting theorem for simple Π11 Sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 433-438
-
- Article
- Export citation
A note on a theorem of Vaught
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 439-440
-
- Article
- Export citation
On the notion of algebraic closedness for noncommutative groups and fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 441-444
-
- Article
- Export citation
Incompleteness of a formal system for infinitary finite-quantifier formulas
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 445-455
-
- Article
- Export citation
A quasi-intumonistic set theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 456-460
-
- Article
- Export citation
A remark on infinitary languages
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 461-462
-
- Article
- Export citation
Nonstandard topology and extensions of monad systems to infinite points
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 463-476
-
- Article
- Export citation
Countable vector spaces with recursive operations Part II1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 477-493
-
- Article
- Export citation
Existence and feasibility in arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 494-508
-
- Article
- Export citation
Reviews
Reviews - Desmond P. Henry. The De grammatico of St. Anselm. The theory of paronymy. Publications in mediaeval studies no. 18. University of Notre Dame Press, Notre Dame, Ind., 1964, XV + 169 pp. - Desmond Paul Henry. Why “Grammaticus”?Archivum latinitatis medii aevi (Bulletin dm Conge), vol. 28 no. 2–3 (1958), pp. 165–180. - Desmond Paul Henry. Saint Anselm's nonsense. Mind, n.s. vol. 72 (1963), pp. 51–61. - Desmond Paul Henry. An Anselmian regress. Notre Dame journal of formal logic, vol. 3 (1962), pp. 193–198.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 509-513
-
- Article
- Export citation
J. L. Austin. How to do things with words. The William James Lectures delivered at Harvard University in 1955. The Clarendon Press, Oxford1962, vii + 166 pp., and Harvard University Press, Cambridge, Mass., 1962, ix + 167 pp. - Jon Wheatley. Austin on implication and entailment. Philosophical studies (Minneapolis), vol. 15 (1964), pp. 46–48. - Bill MathewsJr., Austin on implication and entailment: A reply to Mr. Wheatley. Philosophical studies (Minneapolis), vol. 15 (1964), pp. 88–89.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 513-514
-
- Article
- Export citation
Hans Freudenthal. Analyse mathématique de certaines structures linguistiques. Folia biotheoretica, vol. 5 (1960), pp. 81–89; also La biologie et la philosophie, Quatre communications données à l'occasion du Symposium de Rome, 1–8 avril 1959, E. J. Brill, Leyden 1960, pp. 81–89. - P. Bernays. H. Freudenthal, F. Gonseth, M. Fréchet, J. Ladrière, B. Segre. Discussion. Folia biotheoretica, vol. 5 (1960), pp. 89–95; also La biologie et la philosophie, Quatre communications données à l'occasion du Symposium de Rome, 1–8 avril 1959, E. J. Brill, Leyden 1960b, pp. 89–95.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 514-515
-
- Article
- Export citation
Charles Hartshorne. Ten ontological or modal proofs for God's existence. The logic of perfection and other essays in neoclassical metaphysics, by Charles Hartshorne, The Open Court Publishing Company, La Salle, Illinois, 1962, pp. 28–117.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 515
-
- Article
- Export citation
Arthur N. Prior. Changes in events and changes in things. Papers on time and tense, by Arthur N. Prior, Oxford at the Clarendon Press1968, pp. 1–14. (A reprint of The Lindley lecture, University of Kansas, Lawrence 1962, 13 pp.) - Arthur N. Prior. On spurious egocentricity. Papers on time and tense, by Arthur N. Prior, Oxford at the Clarendon Press1968, pp. 15–25. (Reprinted from Philosophy, vol. 42 (1967), pp. 326–335.) - Arthur N. Prior. The formalities of omniscience. Papers on time and tense, by Arthur N. Prior, Oxford at the Clarendon Press1968, pp. 26–44. (Reprinted from Philosophy, vol. 37 (1962), pp. 114–129.) - Arthur N. Prior. Contemplation and action. Papers on time and tense, by Arthur N. Prior, Oxford at the Clarendon Press1968, pp. 45–50. - Arthur N. Prior. The consequences of actions. Papers on time and tense, by Arthur N. Prior, Oxford at the Clarendon Press1968, pp. 51–58. (Reprinted from Aristotelian Society supplementary volume XXX, London 1956, pp. 91–99.) - Arthur N. Prior. Limited indeterminism. Papers on time and tense, by Arthur N. Prior, Oxford at the Clarendon Press1968, pp. 59–65. (Reprinted from The review of metaphysics, vol. 16 no. 1 (1962), pp. 55–61.) - Arthur N. Prior. Identifiable individuals. Papers on time and tense, by Arthur N. Prior, Oxford at the Clarendon Press1968, pp. 66–77. (Reprinted from The review of metaphysics, vol. 13, no. 4 (1960), pp. 684–696.) - Arthur N. Prior. Time, existence, and identity. Papers on time and tense, by Arthur N. Prior, Oxford at the Clarendon Press1968, pp. 78–87. (Reprinted from Proceedings of the Aristotelian Society, n.s. vol. 66 (1965–66), pp. 183–192.) - Arthur N. Prior. Stratified metric tense logic. Papers on time and tense, by Arthur N. Prior, Oxford at the Clarendon Press1968, pp. 88–97. (Reprinted from Theoria (Lund), vol. 33 (1967), pp. 28–38.) - Arthur N. Prior. The logic of ending time. Papers on time and tense, by Arthur N. Prior, Oxford at the Clarendon Press1968, pp. 98–115. - Arthur N. Prior. Tense logic and the logic of earlier and later. Papers on time and tense, by Arthur N. Prior, Oxford at the Clarendon Press1968, pp. 116–134. - Arthur N. Prior. Quasi-propositions and quasi-individuals. Papers on time and tense, by Arthur N. Prior, Oxford at the Clarendon Press1968, pp. 135–144. - Arthur N. Prior. Tense logic for non-permanent existents. Papers on time and tense, by Arthur N. Prior, Oxford at the Clarendon Press1968, pp. 145–160.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 515-518
-
- Article
- Export citation
G. W. Turner. Time and place logic, a further discussion of A. N. Prior's ‘Thank goodness that's over’ (XXV 343(3)). Philosophy, vol. 36 (1961), pp. 366–367.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 518
-
- Article
- Export citation
Nicholas Rescher. A version of the “master argument” of Diodorus. The journal of philosophy, vol. 63 (1966), pp. 438–445. - Herbert Guerry. Rescher's master argument. The journal of philosophy, vol. 64 (1967), pp. 310–312.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 518-519
-
- Article
- Export citation

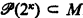 , then
, then 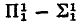 –
– 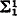 set,
set, 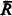 ). The corresponding fact of ordinary recursion theory, namely that any r.e. but not recursive set can be split into two other such sets, was proved by Friedberg [2, Theorem 1], using a clever priority argument. Sacks [7, Corollary 2] then showed that any r.e. but not recursive set is the union of two disjoint r.e. sets neither of which was recursive in the other, a much stronger result. In this paper we attempt to prove the analogous result for
). The corresponding fact of ordinary recursion theory, namely that any r.e. but not recursive set can be split into two other such sets, was proved by Friedberg [2, Theorem 1], using a clever priority argument. Sacks [7, Corollary 2] then showed that any r.e. but not recursive set is the union of two disjoint r.e. sets neither of which was recursive in the other, a much stronger result. In this paper we attempt to prove the analogous result for 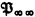 is the result of extending the basic predicate calculus
is the result of extending the basic predicate calculus 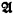 and
and 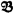 of powers
of powers 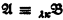 implies
implies 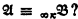 His proofs are by induction on the quantifier rank of formulas and they use an idea which in the case of ordinary first-order language goes back to Ehrenfeucht and Fraïssé. But, as we show, one can easily prove that if
His proofs are by induction on the quantifier rank of formulas and they use an idea which in the case of ordinary first-order language goes back to Ehrenfeucht and Fraïssé. But, as we show, one can easily prove that if