Es ist bekannt, daβ man aus den Funktionen 0 und n + 1 ausgehend, die in der elementaren Zahlentheorie benutzten Funktionen durch eine endliche Kette von Substitutionen und “primitiven Rekursionen” der Form

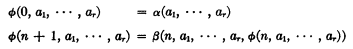
(α(a1, …, ar) und β(n, a1, …, ar, ar+1) bereits eingeführte Funktionen) definieren kann. Aber die “mehrfache Rekursion”, wobei die Rekursion gleichzeitig nach mehreren Variablen läuft, führt aus der so entstehenden Klasse der “primitiv-rekursiven Funktionen” hinaus. Die sogenannten “mehrfachen”, und zwar “k-rekursiven” Funktionen (zu welchen als Spezialfall auch die primitiv-rekursiven Funktionen gehören) lassen sich von gewissen Ausgangsfunktionen ausgehend durch eine endliche Kette von Substitutionen und “k-fachen Rekursionen” (wobei die Rekursion gleichzeitig nach k Variablen läuft) einer gewissen Normalform aufbauen. Die k + 1-fache Rekursion führt für ein jedes k aus der Klasse der k-rekursiven Funktionen hinaus. Das kann mit Hilfe des Diagonalverfahrens bewiesen werden. Das Diagonalverfahren auf sämtliche mehrfach-rekursive Funktionen angewandt (auch wenn man sich auf Funktionen von einer gegebenen Variablenanzahl beschränkt) würde als Beispiel einer nicht mehrfachrekursiven Funktion eine Funktion ergeben, bei der es vom ersten Argument abhängt, wievielstellig die Funktion ist.

Man sagt allgemein, daβ eine Funktion durch irgendeine Rekursion definiert wird, wenn ihr Wert an gewissen Anfangsstellen angegeben, und an einer anderen Stelle aus Werten aufgebaut wird, welche die Funktion an vorherigen Stellen angenommen hat. Es kann aber verschieden vorgeschrieben werden, welche Stellen als Vorgänger einer gegebenen Stelle zu betrachten sind.