In ZFC, the class Ord of ordinals is easily seen to satisfy the definable version of strong inaccessibility. Here we explore deeper ZFC-verifiable combinatorial properties of Ord, as indicated in Theorems A & B below. Note that Theorem A shows the unexpected result that Ord is never definably weakly compact in any model of ZFC.

Theorem A. Let 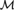${\cal M}$ be any model of ZFC.

1. (1) The definable tree property fails in 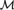${\cal M}$: There is an 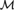${\cal M}$-definable Ord-tree with no 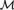${\cal M}$-definable cofinal branch.

2. (2) The definable partition property fails in 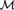${\cal M}$: There is an 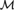${\cal M}$-definable 2-coloring 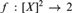$f:{[X]^2} \to 2$ for some 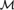${\cal M}$-definable proper class X such that no 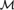${\cal M}$-definable proper classs is monochromatic for f.

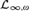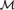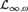3. (3) The definable compactness property for ${{\cal L}_{\infty ,\omega }}$ fails in ${\cal M}$: There is a definable theory ${\rm{\Gamma }}$ in the logic ${{\cal L}_{\infty ,\omega }}$ (in the sense of 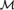${\cal M}$) of size Ord such that every set-sized subtheory of ${\rm{\Gamma }}$ is satisfiable in 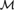${\cal M}$, but there is no 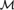${\cal M}$-definable model of ${\rm{\Gamma }}$.

Theorem B. The definable ⋄Ord principle holds in a model 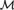${\cal M}$ of ZFC iff 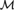${\cal M}$ carries an 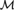${\cal M}$-definable global well-ordering.

Theorems A and B above can be recast as theorem schemes in ZFC, or as asserting that a single statement in the language of class theory holds in all ‘spartan’ models of GB (Gödel-Bernays class theory); where a spartan model of GB is any structure of the form 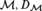$\left( {{\cal M},{D_{\cal M}}} \right)$, where 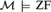${\cal M} \models {\rm{ZF}}$ and 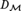${D_{\cal M}}$ is the family of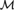${\cal M}$-definable classes. Theorem C gauges the complexity of the collection GBspa of (Gödel-numbers of) sentences that hold in all spartan models of GB.

Theorem C. GBspa is 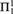${\rm{\Pi }}_1^1$-complete.