Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T05:59:43.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Zero-one laws with variable probability

Published online by Cambridge University Press:  12 March 2014

Joel Spencer
Joel Spencer*
Affiliation:
Departments of Mathematics and Computer Science, Courant Institute, New York, New York, 10012, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

One of this author's favorite theorems has long been the Zero-One law discovered independently by Glebskii et al. [12] and Ron Fagin [10]. Let A be any first-order property of graphs and let µn(A) be the proportion of labelled graphs on n vertices for which A holds. Then

This result has inspired much work by logicians, generally in the direction of showing (1) for some powerful languages. Thus it is known [5] that (1) holds when A is a sentence in fixed point logic and it is known [13] that (1) does not always hold when A is a sentence in second-order monadic logic. Here, however, we explore recent work in a totally different direction. Let G(n, p) denote the random graph on n vertices with edge probability p. (In §2 we define the random structures we will deal with.) A property A is an event in the probability space and Pr[G(n, p) ╞ A] is well defined. When p = 1/2, each labelled graph on n vertices has equal weight so that (1) may be rewritten

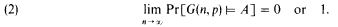
Fagin's proof actually gives that (2) holds for any constant 0 < p < 1.

Type
Survey/expository paper
Information
The Journal of Symbolic Logic , Volume 58 , Issue 1 , March 1993 , pp. 1 - 14
Copyright
Copyright © Association for Symbolic Logic 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Albert, M. H. and Frieze, A. M., Random graph orders, Order, vol. 6 (1989), pp. 19–30.CrossRefGoogle Scholar
[2]Shelah, S. and Spencer, J., Random sparse unary predicates, in preparation.Google Scholar
[3]Compton, K. J., An undecidable problem in finite combinatorics, this Journal, vol. 49 (1984), pp. 842–850Google Scholar
[4]Compton, K. J., Henson, C. W., and Shelah, S., Nonconvergence, undecidability and intractability in asymptotics problems, Annals of Pure and Applied Logic, vol. 36 (1987), pp. 207–224.CrossRefGoogle Scholar
[5]Compton, K. J., 0-1 laws in logic and combinatorics, Algorithms and order (Rival, I., editor), NATO ASI series, Kluwer Academic Publishers, Dordrecht, 1988, pp. 353–383.Google Scholar
[6]Dolan, P., Undecidable statements and random graphs, Annals of Mathematics and Artificial Intelligence, to appear, 1992.Google Scholar
[7]Dolan, P., A zero-one law for a random subset, Random Structures and Algorithms, vol. 2 (1991), pp. 317–326.CrossRefGoogle Scholar
[8]Erdös, P. and Rényi, A., On the evolution of random graphs, Magyar Tud. Mat. Kutató Int. Közl, vol. 5 (1960), pp. 17–60.Google Scholar
[9]Ehrenfeucht, A., An application of games to the completeness problem for formalized theories, Fundamenta Mathematicae, vol. 49 (1961), pp. 129–141.CrossRefGoogle Scholar
[10]Fagin, R., Probabilities in finite models, this Journal, vol. 41 (1976), pp. 50–58.Google Scholar
[11]Fagin, R., Generalized first order spectra and polynomial time recognizable sets, Complexity of Computation (Karp, R. M., editor) SIAM/AMS, Proceedings of Symposia in Applied Mathematics, vol. VII, American Mathematical Society, Providence, RI, 1974, pp. 43–73.Google Scholar
[12]Glebskii, Y. V., Kogan, D. I., Liagonkii, M. I., and Talanov, V. A., Range and degree of realizability of formulas in the restricted predicate calculua, Kibernetica, vol. 5 (1969), pp. 17–27; English translation in Cybernetics, vol. 5, pp. 142–154.Google Scholar
[13]Kaufmann, M. and Shelah, S., On random models of finite power and monadic logic, Discrete Mathematics, vol. 54 (1983), pp. 285–293.CrossRefGoogle Scholar
[14]Ladner, R., Application of model theoretic games to discrete linear orders and finite automata, Information and Control, vol. 33 (1977), pp. 281–303.CrossRefGoogle Scholar
[15]Łuczak, T., First order properties of random posets, Order, vol. 8 (1991), pp. 291–297.CrossRefGoogle Scholar
[16]Łuczak, T. and Spencer, J., When does the zero-one law hold?, Journal of the American Mathematical Society, vol. 4 (1991), pp. 451–468.CrossRefGoogle Scholar
[17]Lynch, J., Probabilities of first-order sentences about unary functions. Transactions of the American Mathematical Society, vol. 287 (1985), pp. 543–568.CrossRefGoogle Scholar
[18]Lynch, J., Almost sure theories. Annals of Mathematical Logic, vol. 18 (1980), pp. 91–135.CrossRefGoogle Scholar
[19]Lynch, J., Properties of sentencess about very sparse random graphs, Random Structures and Algorithms, vol. 3 (1992), pp. 33–54.CrossRefGoogle Scholar
[20]Shelah, S. and Spencer, J., Zero-one laws for sparse random graphs, Journal of the American Mathematical Society, vol. 1 (1988), pp. 97–115.CrossRefGoogle Scholar
[21]Spencer, J., Undecidable probabilities, Random graphs '87 (Karonski, M., Jaworski, J., and Rucinski, A., editors) John Wiley, New York, 1990, pp. 305–311.Google Scholar
[22]Spencer, J., Zero-one laws via the Ehrenfeucht game, Discrete Applied Mathematics, vol. 30 (1991), pp. 235–252.CrossRefGoogle Scholar
[23]Spencer, J., Countable sparse random graphs, Random Structures and Algorithms, vol. 1 (1990), pp. 205–214.CrossRefGoogle Scholar
[24]Spencer, J., Sparse random graphs: A continuum of complete theories, Proceedings of the International Conference on Sets, Graphs and Numbers (D. Miklos, editor), to appear.Google Scholar
[25]Traktenbrot, B. A., Impossibility of an algorithm for the decision problem on finite classes, Doklady Akademii Nauk. S. S. R., vol. 70 (1950), pp. 569–572.Google Scholar
[26]Winkler, P., Random structures and zero-one laws, Finite and Infinite Combinatorics of Sets and Logics (Woodrow, R., editor), NATO ASI Series, Kluwer Academic Publishers, Dordrect, to appear.Google Scholar